Machine Learning Theory Track

Avishek Sen Gupta on 28 March 2021

---

I’ve always been fascinated by Machine Learning. This began in the seventh standard when I discovered a second-hand book on Neural Networks for my ZX Spectrum.

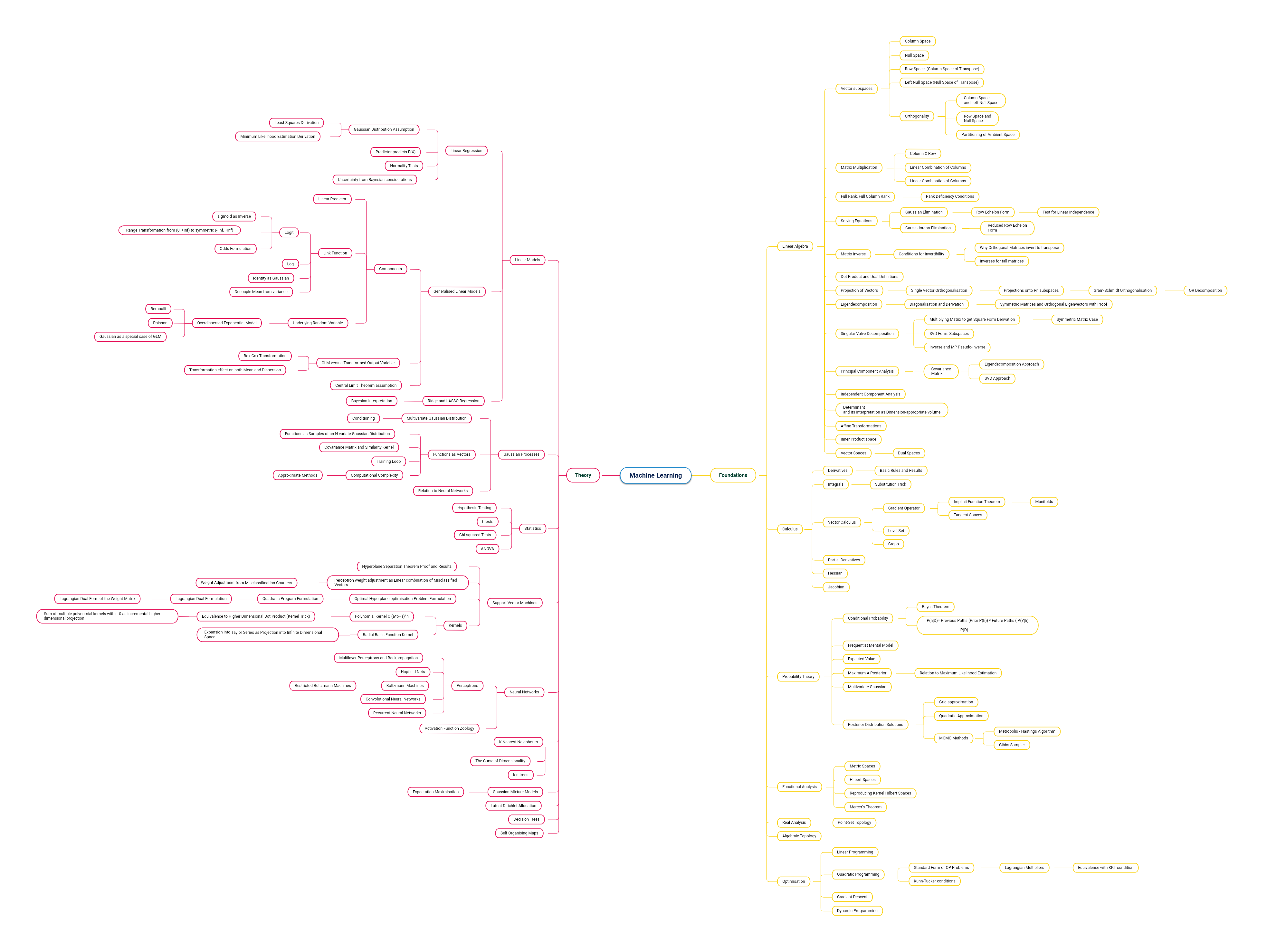
Currently, I’m in the process of sharpening my mathematical intuition and theoretical foundations in some of these areas. This is a current map of stuff I’m working through. Some of the areas which do not have a lot of detail are those whice I need to either revisit, or are very unfamiliar to me.

There are a couple of things worth noting here:

• Intuition is key: I usually spend quite a bit of time understanding the intuition behind some of the mechanics of these methods. It goes without saying that a lot of this does not involve memorising formulae or proofs.
• The Mathematics is just as important: Intuition is a great starting point, but it is not the end. Nothing brings your understanding to a sharper focus than the language of math. Thus this map specifically refers to areas of mathematics that support formalising the intuition in the different areas. Not all areas need to be studied in equal depth, but the key point here is the development of mathematical maturity, so that you do not balk when an equation is thrown at you.
• The implementation is also important: I hope to demonstrate many of the ML techniques through actual implementations in code. This can take one of two forms. On one end, you have the basic algorithmic implementation, which you could do in any programming language. At the other end, we are talking of scaling of ML techniques, and that will require using a suitable framework, like Spark.
• The map is not exhaustive: I’m continuously adding to my understanding, and learning new mathematical concepts/techniques, so expect this list to evolve. I have not included time series analysis and the associated mathematics (Convolution, Laplace and Fourier Transforms) yet. Ultimately, I hope for this list to be a valuable study tool for myself to gauge my progress. If it helps you map out areas you want to focus on in your ML journey, feel free to use this.

Note: Click the image below to open the larger version.

Let’s try to unpack some of the relationships between the mathematics areas and the ML application areas.

• Linear Algebra: You will need this for almost any Machine Learning technique. This is due to the fact that almost every ML problem is formulated in terms of matrices and vectors (and their combinations). Almost every problem’s solution is stated in the form of some condition in the Linear Algebra landscape. Concepts like null space, quadratic form assume importance. Specific concepts in Linear Algebra also contribute hugely to simplification of calculations (eg: diagonisation) as well as valuable analytical insights (eg: Principal Components Analysis).

• Probability: A lot of ML solutions have several underlying assumptions. One of the most important assumptions is how the data is distributed. This probability distribution dictates whether the theoretical solution needs to take extra steps (eg: Generalised Linear Models), or whether the solution can be obtained in a closed form or not (eg, Maximum Likelihood Estimation). Specific Machine Learning techniques are probabilistic at their core (eg: Gaussian Mixture Models).

• Optimisation: This is a huge topic, but I will point out a few areas definitely worth studying. Gradient Descent (or Ascent) is a very important heuristic approach to maximising/minimising cost when no closed form solutions are available. A lot of Machine Learning techniques directly or indirectly state the problem to be solved using Linear Programming or Quadratic Programming (eg: Support Vector Machines). Restatements of optimisation problems using their duals (eg: Langrangian Multipliers) can also lead to significant reduction in computation complexity (eg: Kernel Trick)

• Calculus: Even an undergraduate level of understanding of calculus will benefit tremendously. Mostly, calculus is used to derive conditions of maxima/minima. Differential Calculus and Vector Calculus underlie derivations of almost every optimisation algorithm (eg: Gradient Descent). Integrals are most commonly observed in probability derivations, and partial differentials are usually encountered routinely in problems involving more than one variable. Hessian matrices (calculus + algebra) are used in large-scale optimisation problems (eg: Newton-Raphson method).

• Real and Functional Analysis: Every Machine Learning problem exists in a conceptual space, as do their solutions. These spaces are endowed with many properties, like distance, inner product. These properties are intuitive because we are familiar with Euclidean space; however lots of results in Mathematics are based on definitions of these concepts which can vary based upon the problem at hand. To prove that any ML algorithm works, or that a solution exists in the first place, proofs on what is and is not possible in these spaces, is a central facet of Machine Learning theory. Most people overlook this aspect mostly, which makes sense: engineers are mostly concerned about results. However, even a cursory understanding of these subjects will provide a lot of insight that cannot be understood through layman’s intuition alone.

Other posts will attempt to disseminate some of this intuition, with the necessary math.

---