Total Internal Reflection
Technology and Art
Code
Contact
Mathematics of Machine Learning for the Working Engineer
Machine Learning Theory Track
(Click the image below to see the full-size image)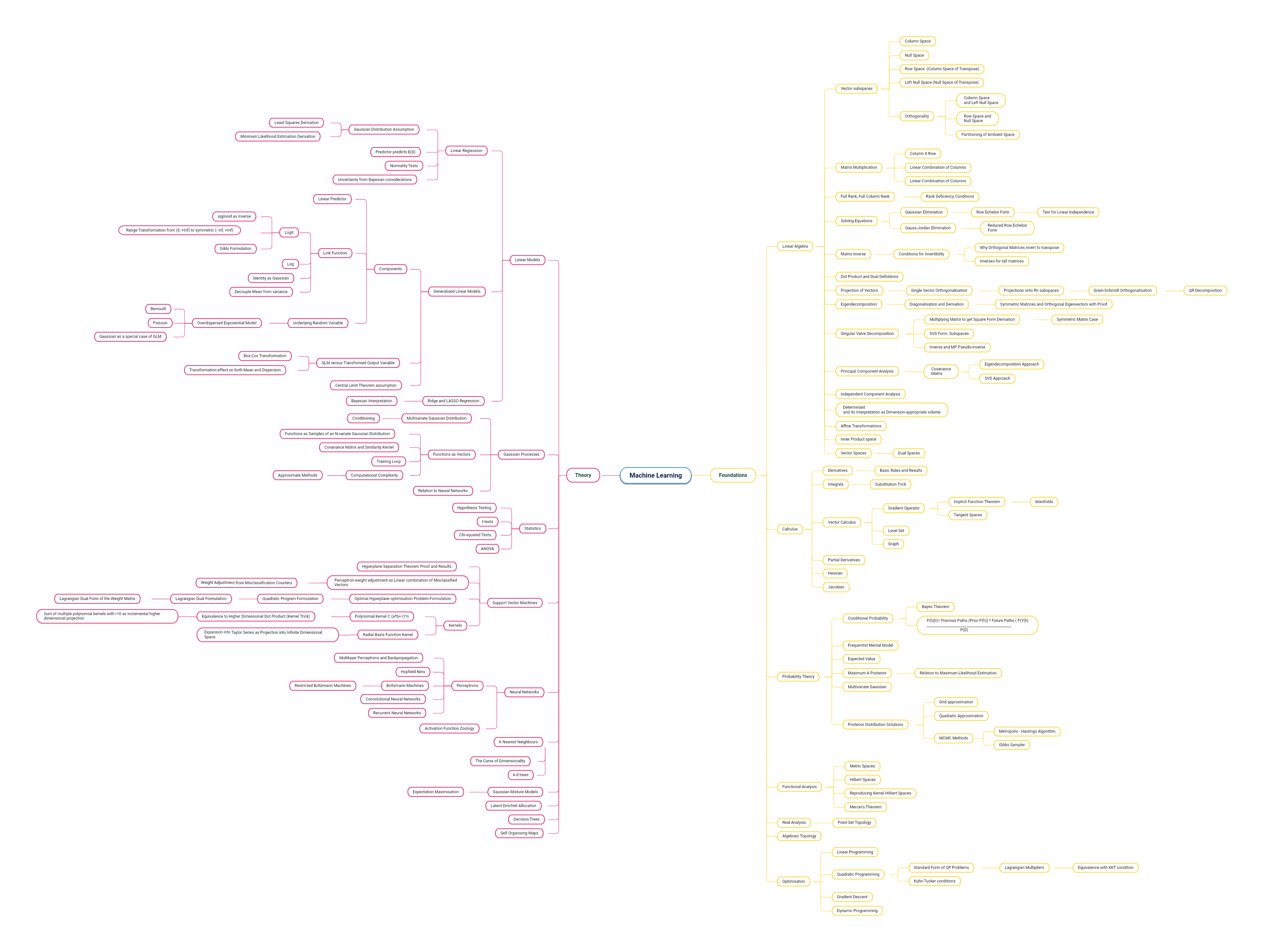
Transformers using PyTorch : Worklog Part 2
14 January 2023We continue looking at the Transformer architecture from where we left from Part 1. When we’d stopped, we’d set up the Encoder stack, but had stopped short of adding positional encoding, and starting work on the Decoder stack. In this post, we will focus on setting up the training cycle.
Tags: Machine Learning, PyTorch, Programming, Deep Learning, TransformersPlenoxels and Neural Radiance Fields using PyTorch: Part 6
27 December 2022This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
Tags: Machine Learning, PyTorch, Programming, Neural Radiance Fields, Machine VisionPlenoxels and Neural Radiance Fields using PyTorch: Part 5
19 December 2022This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
Tags: Machine Learning, PyTorch, Programming, Neural Radiance Fields, Machine VisionPlenoxels and Neural Radiance Fields using PyTorch: Part 4
18 December 2022This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
Tags: Machine Learning, PyTorch, Programming, Neural Radiance Fields, Machine VisionPlenoxels and Neural Radiance Fields using PyTorch: Part 3
7 December 2022This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
Tags: Machine Learning, PyTorch, Programming, Neural Radiance Fields, Machine VisionPlenoxels and Neural Radiance Fields using PyTorch: Part 2
5 December 2022This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
Tags: Machine Learning, PyTorch, Programming, Neural Radiance Fields, Machine VisionPlenoxels and Neural Radiance Fields using PyTorch: Part 1
4 December 2022This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
Tags: Machine Learning, PyTorch, Programming, Neural Radiance Fields, Machine VisionTransformers using PyTorch : Worklog Part 1
29 November 2022It may seem strange that I’m jumping from implementing a simple neural network into Transformers. I will return to building up the foundations of neural networks soon enough: for the moment, let’s build a Transformer using PyTorch.
Tags: Machine Learning, PyTorch, Programming, Deep Learning, TransformersThe No-Questions Asked Guide to PyTorch : Part 1
27 November 2022Programming guides are probably the first posts to become obsolete, as APIs are updated. Regardless, we will look at building simple neural networks in PyTorch. We won’t be starting from models with a million parameters, however. We will proceed from the basics, starting with a single neuron, talk a little about the tensor notation and how that relates to our usual mathematical notation of representing everything with column vectors, and scale up from there.
Tags: Machine Learning, PyTorch, Programming, Neural NetworksGaussian Processes: Theory
10 September 2021In this article, we will build up our mathematical understanding of Gaussian Processes. We will understand the conditioning operation a bit more, since that is the backbone of inferring the posterior distribution. We will also look at how the covariance matrix evolves as training points are added.
Tags: Theory, Gaussian Processes, Probability, Machine LearningGaussian Processes: Intuition
6 September 2021In this article, we will build up our intuition of Gaussian Processes, and try to understand how it models uncertainty about data it has not encountered yet, while still being useful for regression. We will also see why the Covariance Matrix (and consequently, the Kernel) is a fundamental building block of our assumptions around the data we are trying to model.
Tags: Theory, Gaussian Processes, Probability, Machine LearningNon-Linear Support Vector Machines: Radial Basis Function Kernel and the Kernel Trick
7 August 2021This article builds upon the previous material on kernels and Support Vector Machines to introduce some simple examples of Reproducing Kernels, including a simplified version of the frequently-used Radial Basis Function kernel. Beyond that, we finally look at the actual application of kernels and the so-called Kernel Trick to avoid expensive computation of projections of data points into higher-dimensional space, when working with Support Vector Machines.
Tags: Machine Learning, Kernels, Theory, Functional Analysis, Support Vector MachinesKernel Functions with Reproducing Kernel Hilbert Spaces
20 July 2021This article uses the previous mathematical groundwork to discuss the construction of Reproducing Kernel Hilbert Spaces. We’ll make several assumptions that have been proved and discussed in those articles. There are multiple ways of discussing Kernel Functions, like the Moore–Aronszajn Theorem and Mercer’s Theorem. We may discuss some of those approaches in the future, but here we will focus on the constructive approach here to characterise Kernel Functions.
Tags: Machine Learning, Kernels, Theory, Functional Analysis, Linear AlgebraKernel Functions: Functional Analysis and Linear Algebra Preliminaries
17 July 2021This article lays the groundwork for an important construction called Reproducing Kernel Hilbert Spaces, which allows a certain class of functions (called Kernel Functions) to be a valid representation of an inner product in (potentially) higher-dimensional space. This construction will allow us to perform the necessary higher-dimensional computations, without projecting every point in our data set into higher dimensions, explicitly, in the case of Non-Linear Support Vector Machines, which will be discussed in the upcoming article.
Tags: Machine Learning, Kernels, Theory, Functional Analysis, Linear AlgebraThe Cholesky and LDL* Factorisations
8 July 2021This article discusses a set of two useful (and closely related) factorisations for positive-definite matrices: the Cholesky and the \(LDL^T\) factorisations. Both of them find various uses: the Cholesky factorisation particularly is used when solving large systems of linear equations.
Tags: Machine Learning, Theory, Linear AlgebraThe Gram-Schmidt Orthogonalisation
27 May 2021We discuss an important factorisation of a matrix, which allows us to convert a linearly independent but non-orthogonal basis to a linearly independent orthonormal basis. This uses a procedure which iteratively extracts vectors which are orthonormal to the previously-extracted vectors, to ultimately define the orthonormal basis. This is called the Gram-Schmidt Orthogonalisation, and we will also show a proof for this.
Tags: Machine Learning, Linear Algebra, Proofs, TheorySupport Vector Machines from First Principles: Linear SVMs
10 May 2021We have looked at how Lagrangian Multipliers and how they help build constraints as part of the function that we wish to optimise. Their relevance in Support Vector Machines is how the constraints about the classifier margin (i.e., the supporting hyperplanes) is incorporated in the search for the optimal hyperplane.
Tags: Machine Learning, Support Vector Machines, Optimisation, TheoryQuadratic Optimisation: Lagrangian Dual, and the Karush-Kuhn-Tucker Conditions
10 May 2021This article concludes the (very abbreviated) theoretical background required to understand Quadratic Optimisation. Here, we extend the Lagrangian Multipliers approach, which in its current form, admits only equality constraints. We will extend it to allow constraints which can be expressed as inequalities.
Tags: Machine Learning, Quadratic Optimisation, Linear Algebra, Optimisation, TheoryCommon Ways of Looking at Matrix Multiplications
29 April 2021We consider the more frequently utilised viewpoints of matrix multiplication, and relate it to one or more applications where using a certain viewpoint is more useful. These are the viewpoints we will consider.
Tags: Machine Learning, Linear Algebra, TheoryQuadratic Optimisation using Principal Component Analysis as Motivation: Part Two
28 April 2021We pick up from where we left off in Quadratic Optimisation using Principal Component Analysis as Motivation: Part One. We treated Principal Component Analysis as an optimisation, and took a detour to build our geometric intuition behind Lagrange Multipliers, wading through its proof to some level.
Tags: Machine Learning, Quadratic Optimisation, Linear Algebra, Principal Components Analysis, Optimisation, TheoryVector Calculus: Lagrange Multipliers, Manifolds, and the Implicit Function Theorem
24 April 2021In this article, we finally put all our understanding of Vector Calculus to use by showing why and how Lagrange Multipliers work. We will be focusing on several important ideas, but the most important one is around the linearisation of spaces at a local level, which might not be smooth globally. The Implicit Function Theorem will provide a strong statement around the conditions necessary to satisfy this.
Tags: Machine Learning, Optimisation, Vector Calculus, Lagrange Multipliers, TheoryVector Calculus: Graphs, Level Sets, and Constraint Manifolds
20 April 2021In this article, we take a detour to understand the mathematical intuition behind Constrained Optimisation, and more specifically the method of Lagrangian multipliers. We have been discussing Linear Algebra, specifically matrices, for quite a bit now. Optimisation theory, and Quadratic Optimisation as well, relies heavily on Vector Calculus for many of its results and proofs.
Tags: Machine Learning, Vector Calculus, TheoryQuadratic Optimisation using Principal Component Analysis as Motivation: Part One
19 April 2021This series of articles presents the intuition behind the Quadratic Form of a Matrix, as well as its optimisation counterpart, Quadratic Optimisation, motivated by the example of Principal Components Analysis. PCA is presented here, not in its own right, but as an application of these two concepts. PCA proper will be presented in another article where we will discuss eigendecomposition, eigenvalues, and eigenvectors.
Tags: Machine Learning, Quadratic Optimisation, Linear Algebra, Principal Components Analysis, Optimisation, TheoryRoad to Gaussian Processes
17 April 2021This article aims to start the road towards a theoretical intuition behind Gaussian Processes, another Machine Learning technique based on Bayes’ Rule. However, there is a raft of material that I needed to understand and relearn before fully appreciating some of the underpinnings of this technique.
Tags: Machine Learning, Gaussian Processes, TheorySupport Vector Machines from First Principles: Part One
14 April 2021We will derive the intuition behind Support Vector Machines from first principles. This will involve deriving some basic vector algebra proofs, including exploring some intuitions behind hyperplanes. Then we’ll continue adding to our understanding the concepts behind quadratic optimisation.
Tags: Machine Learning, Support Vector Machines, TheoryDot Product: Algebraic and Geometric Equivalence
11 April 2021The dot product of two vectors is geometrically simple: the product of the magnitudes of these vectors multiplied by the cosine of the angle between them. What is not immediately obvious is the algebraic interpretation of the dot product.
Tags: Machine Learning, Linear Algebra, Dot Product, TheoryLinear Regression: Assumptions and Results using the Maximum Likelihood Estimator
5 April 2021Let’s look at Linear Regression. The “linear” term refers to the fact that the output variable is a linear combination of the input variables.
Tags: Machine Learning, Linear Regression, Maximum Likelihod Estimator, Theory, ProbabilityMatrix Rank and Some Results
4 April 2021I’d like to introduce some basic results about the rank of a matrix. Simply put, the rank of a matrix is the number of independent vectors in a matrix. Note that I didn’t say whether these are column vectors or row vectors; that’s because of the following section which will narrow down the specific cases (we will also prove that these numbers are equal for any matrix).
Tags: Machine Learning, Linear Algebra, TheoryAssorted Intuitions about Matrices
3 April 2021Some of these points about matrices are worth noting down, as aids to intuition. I might expand on some of these points into their own posts.
Tags: Machine Learning, Linear Algebra, TheoryMatrix Outer Product: Columns-into-Rows and the LU Factorisation
2 April 2021We will discuss the Column-into-Rows computation technique for matrix outer products. This will lead us to one of the important factorisations (the LU Decomposition) that is used computationally when solving systems of equations, or computing matrix inverses.
Tags: Machine Learning, Linear Algebra, TheoryIntuitions about the Orthogonality of Matrix Subspaces
2 April 2021This is the easiest way I’ve been able to explain to myself around the orthogonality of matrix spaces. The argument will essentially be based on the geometry of planes which extends naturally to hyperplanes.
Tags: Machine Learning, Linear Algebra, TheoryMatrix Outer Product: Value-wise computation and the Transposition Rule
1 April 2021We will discuss the value-wise computation technique for matrix outer products. This will lead us to a simple sketch of the proof of reversal of order for transposed outer products.
Tags: Machine Learning, Linear Algebra, TheoryMatrix Outer Product: Linear Combinations of Vectors
30 March 2021Matrix multiplication (outer product) is a fundamental operation in almost any Machine Learning proof, statement, or computation. Much insight may be gleaned by looking at different ways of looking matrix multiplication. In this post, we will look at one (and possibly the most important) interpretation: namely, the linear combination of vectors.
Tags: Machine Learning, Linear Algebra, TheoryVectors, Normals, and Hyperplanes
29 March 2021Linear Algebra deals with matrices. But that is missing the point, because the more fundamental component of a matrix is what will allow us to build our intuition on this subject. This component is the vector, and in this post, I will introduce vectors, along with common notations of expression.
Tags: Machine Learning, Linear Algebra, TheoryMachine Learning Theory Track
28 March 2021I’ve always been fascinated by Machine Learning. This began in the seventh standard when I discovered a second-hand book on Neural Networks for my ZX Spectrum.
Tags: Machine Learning, Theory