Assorted Intuitions about Matrices

Avishek Sen Gupta on 3 April 2021

---

Some of these points about matrices are worth noting down, as aids to intuition. I might expand on some of these points into their own posts.

• A matrix is a collection of column vectors.
• A matrix is a collection of row vectors.
• A matrix is a linear transformation, with its column vectors being the new basis.
• A matrix \(A\) cannot be inverted (i.e., it does not have a unique inverse) if any of its column vectors are linearly dependent on the others.
  • This is because, then there will always be a non-zero vector solution which will lose all of its components to zero; and there is no way to reverse that operation to recover the original vector.
  • As an illustration, if you have an \(n \times n\) matrix \(A\), and an \(n \times 1\) vector \(\vec{v}\), and that the 1st and 2nd column vectors of \(A\) are linearly dependent, but the rest of them are linearly independent. Then there exists a vector \(\vec{v_0}\) of the form \((a,b,0,0,...,0_n)\) where the scalars \(a\) and \(b\) force the first two column vectors to cancel out to zero in the result; and since the rest of the vector components are zero to begin with, the result will end up all zeros.
  • Mathematically, this means if there exists a nonzero \(x\), such that \(Ax=0\), \(A\) is not invertible.
• The dot product of two vectors is a linear transformation of the right vector into the number line, with the individual scalar components of the left vector being the basis vectors on this one-dimensional number line.

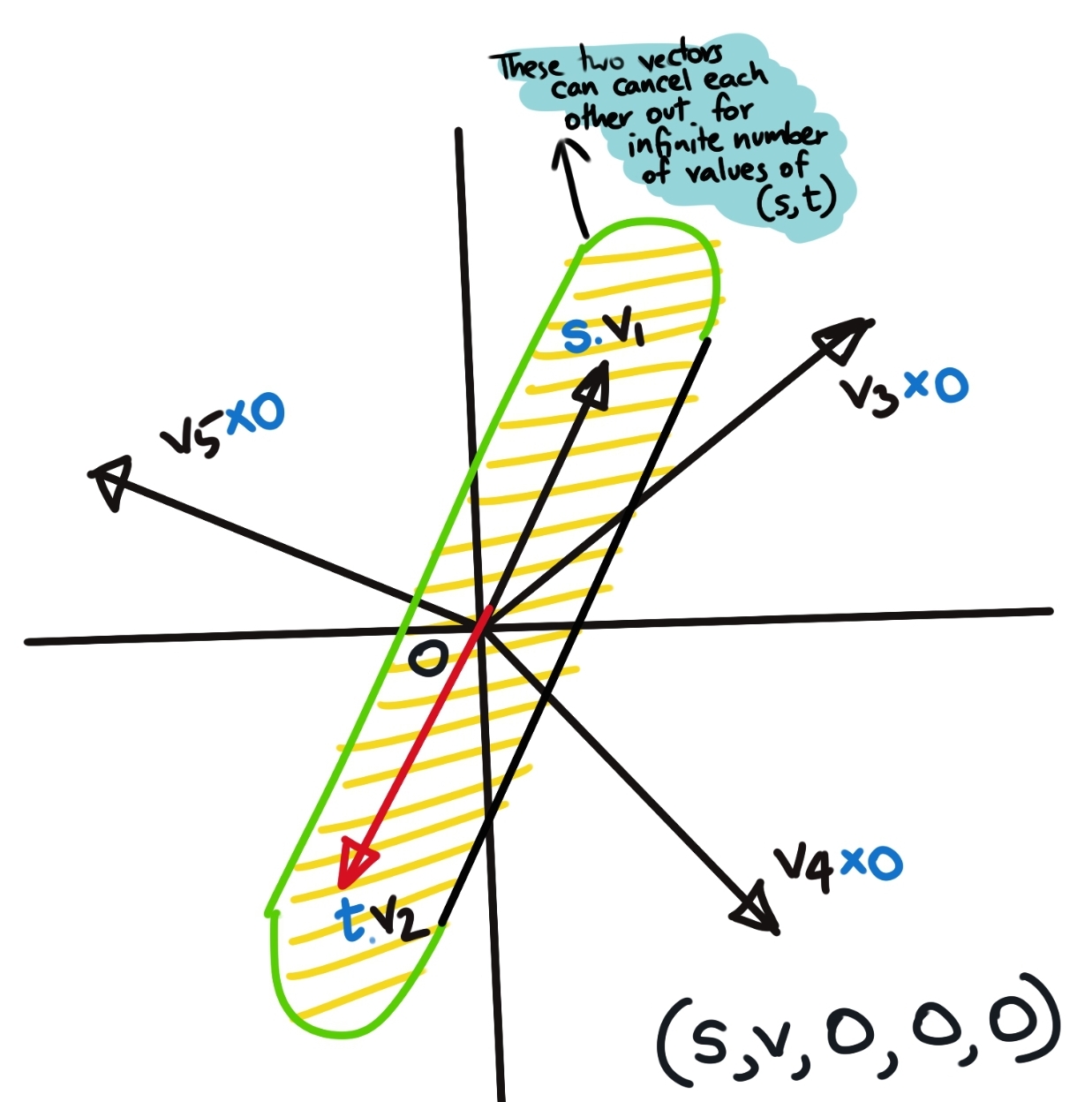
Note that the above diagram is not mathematically correct. I drew 5 basis vectors in 2D space, and you cannot have more than 2 linearly independent basis vectors in two dimensions. This diagram is simply for illustration purposes.

• The determinant of a matrix is essentially the volume spanned by the basis vectors formed by its columns. A degenerate matrix has a determinant of zero because the measurement of this “hypervolume” on one axis becomes zero.

• The left null space of a matrix represents the set of normal vectors for the hyperplane defined by the column space of this matrix. This is because by definition, all vectors in the left null space are orthogonal to the column space. Thus, any vector in the left null space also represents the actual geometric equation of the hyperplane defined by the column space.

---