Important Inequalities in Functional Analysis

Avishek Sen Gupta on 27 September 2021

---

Continuing my self-study of Functional Analysis, this post describes proofs for the following important inequalities in the subject:

• Young’s Inequality
• Hölder’s Inequality
• Minkowski’s Inequality

The paths of the proofs closely follow Erwin Kreyszig’s Introductory Functional Analysis with Applications.

Young’s Inequality

We begin with the idea of conjugate exponents, which we call \(p\) and \(q\), related like so:

\[\frac{1}{p} + \frac{1}{q} = 1 \\ \Rightarrow q + p = pq \\ \Rightarrow q + p = pq \\ \Rightarrow p(q - 1)= q \\ \Rightarrow p=\frac{q}{q-1} \\ \Rightarrow 1-p=1-\frac{q}{q-1} \\ \Rightarrow 1-p=\frac{q-1-q}{q-1}\] \[\begin{equation} \Rightarrow 1-p=\frac{1}{1-q} \label{eq:conjugate-exponents-property-1} \end{equation}\]

where \(p>1\). We now use these exponents in the following identity:

\[u=t^{p-1}\]

We also record the following implication.

\[t=u^{\frac{1}{p-1}} \\ \Rightarrow t=u^{q-1}\]

For \(p=2\), we get \(u=t\), which is the equation of the straight line \(x=y\). The above follows from \(\eqref{eq:conjugate-exponents-property-1}\).

Let \(\alpha, \beta >0: \alpha, \beta \in \mathbb{R}\), then in \(\mathbb{R}^2\), \(\alpha\beta\) describes the area of a rectangle. Let us plot the graph of \(u=t^{p-1}\) for \(p=2\), so that \(u=t\).

If we integrate \(\displaystyle\int\limits_0^\alpha u.dt=\int\limits_0^\alpha t^{p-1}.dt\), and \(\displaystyle\int\limits_0^\alpha t.du=\int\limits_0^\alpha u^{q-1}.du\), we can compute an area like this:

\[\begin{align*} S &= \int\limits_0^\alpha t^{p-1}.dt + \int\limits_0^\alpha u^{q-1}.du \\ &= \frac{\alpha^2}{2} + \frac{\beta^2}{2} \end{align*}\]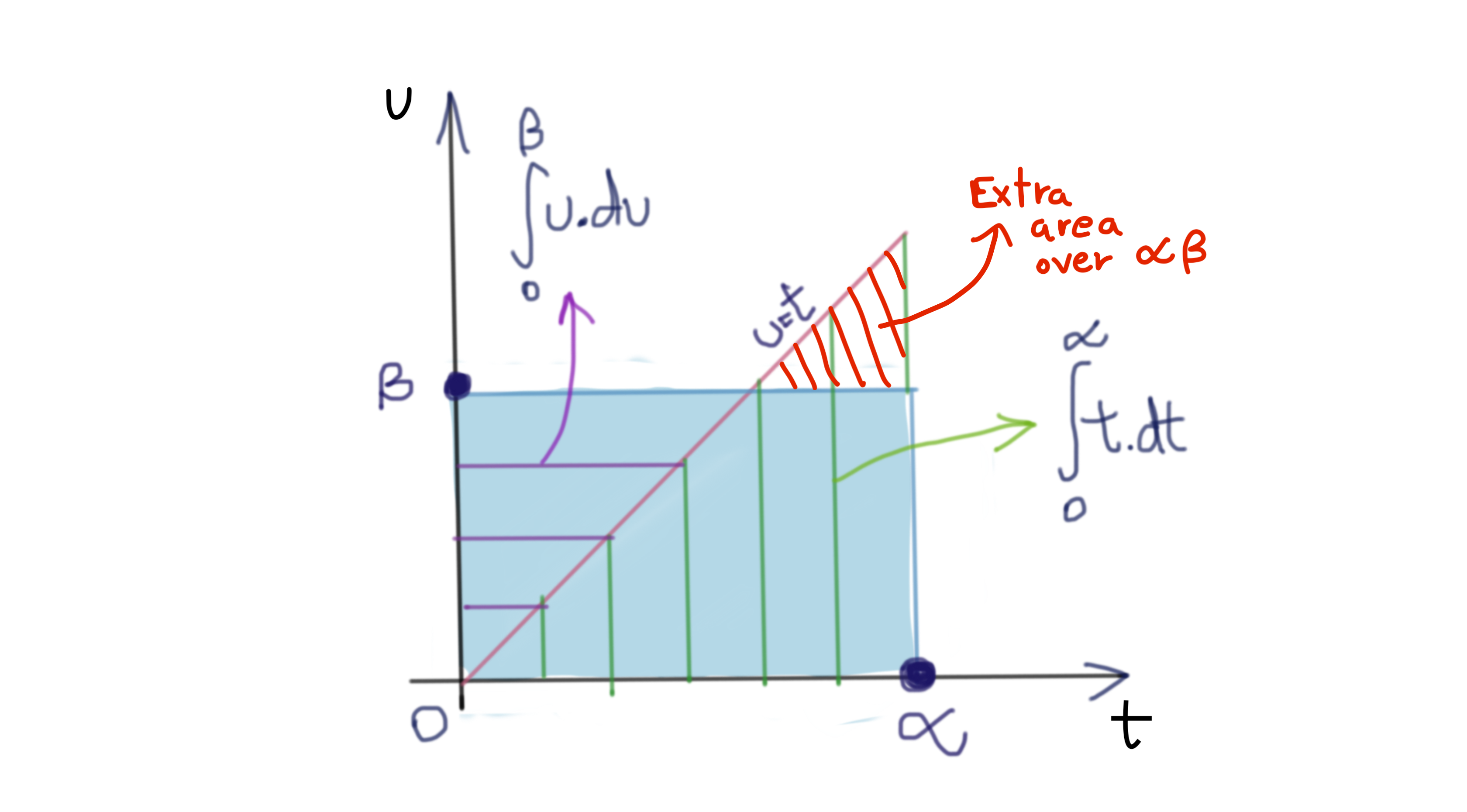

You will notice that regardless of the choice of \(\alpha, \beta\), there will always be a small portion of \(S\) which is bigger than \(\alpha\beta\). The only situation in which there is no extra area is when \(\alpha=\beta\). Therefore, we can say that:

\[\alpha \beta \leq \frac{\alpha^2}{2} + \frac{\beta^2}{2}\]

This less-than-or-equal relation carries over to other values of \(p\) where \(u=t^{p-1}\) is an exponential graph. The following two graphs illustrate how this is always true.

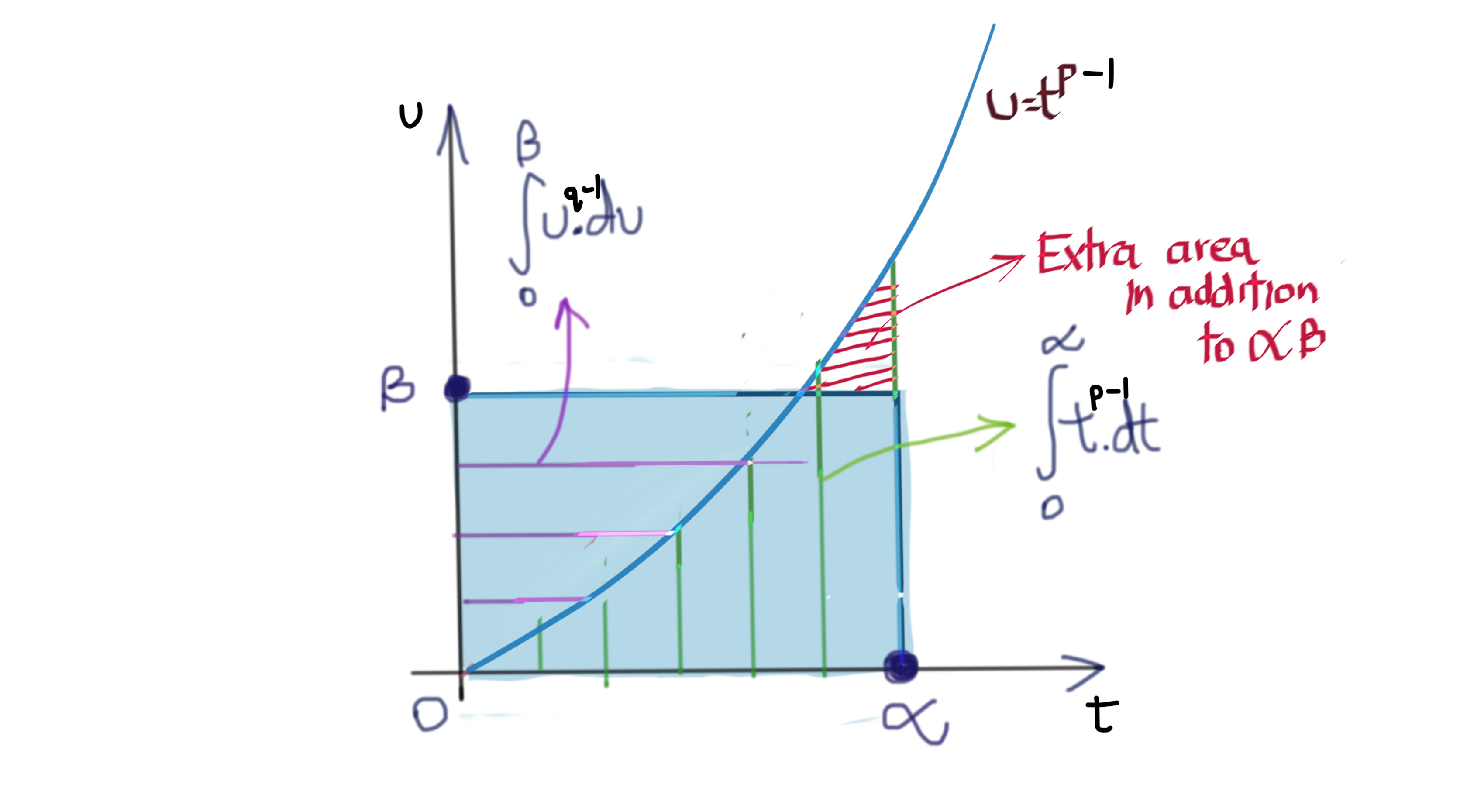
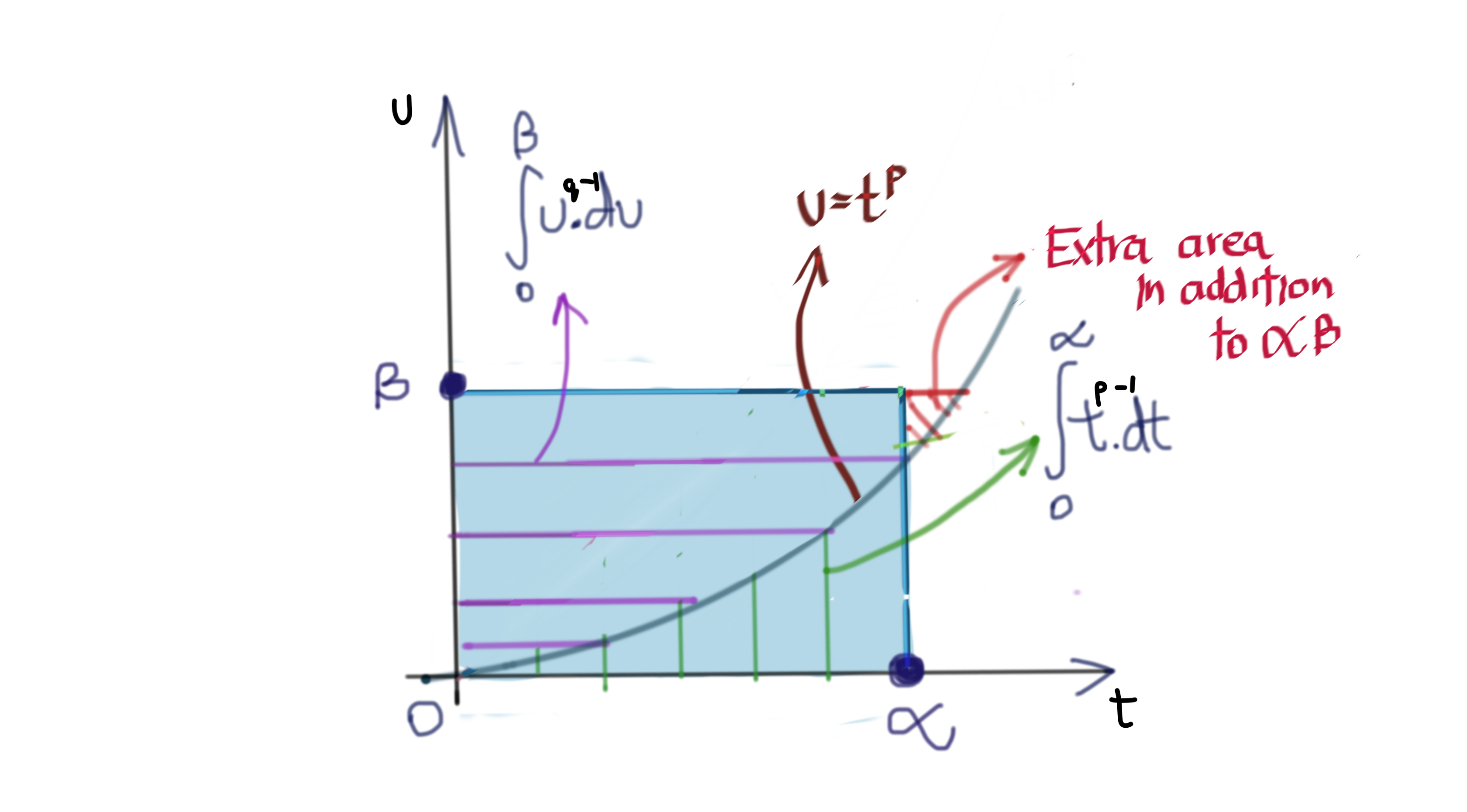
Thus, we can conclude that:

\[\begin{equation} \alpha \beta \leq \frac{\alpha^p}{p} + \frac{\beta^q}{q} \label{eq:youngs-inequality} \end{equation}\]

\(\eqref{eq:youngs-inequality}\) is called Young’s Equality, and we will use it to prove Hölder’s Inequality next.

A more interesting way to think about (and remember) Young’s Equality is to note that \(\text{log }(x)\) is a concave function, therefore by the definition of concavity, we have:

\[f(\alpha x^p + (1 - \alpha) y^q) \geq \alpha f(x^p) + (1-\alpha) f(y^q) \\ \text{log }(\alpha x^p + (1 - \alpha) y^q) \geq \alpha\text{log }(x^p) + (1-\alpha) \text{log }(y^q) \\ \text{log }\left(\frac {x^p}{p} + \frac {y^q}{q}\right) \geq \frac{\text{log }(x^p)}{p} + \frac{\text{log }(y^q)}{q} = \text{log }(x^{(p/p)}) + \text{log }(y^{(q/q)}) \\ \text{log }\left(\frac {x^p}{p} + \frac {y^q}{q}\right) \geq \text{log }(xy) \\ \Rightarrow xy \leq \left(\frac {x^p}{p} + \frac {y^q}{q}\right)\]

Hölder’s Inequality

We look at \(\ell^p\) spaces now. Briefly recapping, \(\ell^p\) spaces are spaces of sequences. A sequence \(\xi=\{\xi_1, \xi_2, \cdots\} \in\ell^p\) must satisfy the following condition:

\[\sum\limits_{i=1}^\infty{|\xi_i|}^p<\infty\]

The norm \(\|\bullet\|\) in \(\ell^p\) spaces is usually defined as:

\[\|\bullet\|={\left(\sum\limits_{i=1}^\infty{|\xi_i|}^p\right)}^{\frac{1}{p}}\]

which induces the distance metric between two sequences \(\xi, \eta \in \ell_p\):

\[d(\xi,\eta)={\left(\sum\limits_{i=1}^\infty{|\xi_i-\eta_i|}^p\right)}^{\frac{1}{p}}\]

Pick any \(\xi,\eta\in\ell^p\).

Let us pick any two corresponding terms in \(\xi\) and \(\eta\), and let \(\alpha=\vert\xi_i\vert\) and \(\beta_i=\vert\eta\vert\), since we cannot guarantee these terms will be positive.

Then, from Young’s Inequality \(\eqref{eq:youngs-inequality}\), we get:

\[|\xi_i||\eta_i| \leq \frac{ {|\xi_i|}^p}{p} + \frac{ {|\eta_i|}^q}{q} \\ \Rightarrow |\xi_i\eta_i| \leq \frac{ {|\xi_i|}^p}{p} + \frac{ {|\eta_i|}^q}{q}\]

Summing over all \(i\), we get:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty|\xi_i\eta_i| \leq \frac{\sum\limits_{i=1}^\infty{|\xi_i|}^p}{p} + \frac{\sum\limits_{i=1}^\infty{|\eta_i|}^q}{q} \label{eq:holders-youngs-inequality-application} \end{equation}\]

What we’d like to do is prove that: \(\displaystyle\sum\limits_{i=1}^\infty\vert\xi_i\eta_i\vert \leq 1\). The only identity immediately available is the conjugate exponent identity, namely:

\[\frac{1}{p} + \frac{1}{q} = 1\]

In order to be able to set the RHS of \(\eqref{eq:holders-youngs-inequality-application}\), we need the following condition:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty{ {\vert\xi_i\vert}^p}=\displaystyle\sum_{i=1}^\infty{ {\vert\eta_i\vert}^q}=1 \label{eq:holders-unity-condition} \end{equation}\]

Let us then assume \(\eqref{eq:holders-unity-condition}\). Then, \(\eqref{eq:holders-youngs-inequality-application}\) becomes:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty|\xi_i\eta_i| \leq 1 \label{eq:holders-less-than-unity-condition} \end{equation}\]

We need to determine what sort of \(\xi\) and \(\eta\) can satisfy this condition. Let’s take \(\xi\) as an example. We have:

\[\xi=(\xi_1, \xi_2, \cdots)\]

Remember the norm for \(\ell^p\) spaces? Here it is again:

\[\|\bullet\|={\left(\sum\limits_{i=1}^\infty{|\xi_i|}^p\right)}^{\frac{1}{p}}\]

If we divide each term in \(\xi\) by its norm:

\[\begin{equation} \xi_i = \frac{\bar\xi_i}{ {\left(\sum\limits_{i=1}^\infty{|\bar{\xi_i}|}^p\right)}^{\frac{1}{p}}} \label{eq:holders-sequence-scale-factor} \end{equation}\]

Then, from \(\eqref{eq:holders-unity-condition}\), we get:

\[\displaystyle\sum\limits_{i=1}^\infty{ {|\xi_i|}^p}=\frac{1}{ \sum\limits_{i=1}^\infty{|\bar{\xi_i}|}^p} \left({|\bar{\xi_1}|}^p + {|\bar{\xi_2}|}^p + \cdots\right) \\ =\frac{\sum\limits_{i=1}^\infty{|\bar{\xi_i}|}^p}{\sum\limits_{i=1}^\infty{|\bar{\xi_i}|}^p} = 1\]

which satisfies condition \(\eqref{eq:holders-unity-condition}\), regardless of which sequence \(\bar{\xi}\) we choose from \(\ell^p\).

Applying the same logic to \(\eta_i\), and substituting \(\eqref{eq:holders-sequence-scale-factor}\) into \(\eqref{eq:holders-less-than-unity-condition}\), we get:

\[\displaystyle\sum\limits_{i=1}^\infty |\bar\xi_i \bar\eta_i| \leq {\left(\displaystyle\sum\limits_{i=1}^\infty{ {|\bar\xi_i|}^p}\right)}^{\frac{1}{p}} \bullet {\left(\displaystyle\sum\limits_{i=1}^\infty{ {|\bar\eta_i|}^q}\right)}^{\frac{1}{q}}\]

Removing the overbars from \(\bar\xi_i\) \(\bar\eta_i\) to indicate any two sequences in an \(\ell^p\) space, we get:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty |\xi_i \eta_i| \leq {\left(\displaystyle\sum\limits_{i=1}^\infty{ {|\xi_i|}^p}\right)}^{\frac{1}{p}} \bullet {\left(\displaystyle\sum\limits_{i=1}^\infty{ {|\eta_i|}^q}\right)}^{\frac{1}{q}} \label{eq:holders-inequality} \end{equation}\]

The result \(\eqref{eq:holders-inequality}\) is referred to as Hölder’s Inequality.

In the case of \(p=2\), \(q=2\); this special case is called the Cauchy-Schwarz Inequality, which is:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty |\xi_i \eta_i| \leq \sqrt{\left(\displaystyle\sum\limits_{i=1}^\infty{ {|\xi_i|}^2}\right) \bullet \left(\displaystyle\sum\limits_{i=1}^\infty{ {|\eta_i|}^2}\right)} \label{eq:cauchy-schwarz-inequality} \end{equation}\]

Hölder’s Inequality will be used to prove Minkowski’s Inequality next.

Minkowski’s Inequality

Minkowski’s Inequality is a generalisation of the Triangle Inequality. As usual, we assume \(\xi, \eta \in \ell^p\). We start with writing (for economy of notation):

\[\omega_i=|\xi_i+\eta_i| \\ \Rightarrow {\omega_i}^p={|\xi_i+\eta_i|}^p \\ \Rightarrow {\omega_i}^p={\omega_i}^{p-1}|\xi_i+\eta_i|\]

Summing up over \(i\), we get:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty{\omega_i}^p = \displaystyle\sum\limits_{i=1}^\infty {\omega_i}^{p-1}|\xi_i+\eta_i| \label{eq:minkowski-separated-summed} \end{equation}\]

Now applying the Triangle Inequality to the second term on the RHS of \(\eqref{eq:minkowski-separated-summed}\), we get:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty{\omega_i}^p = \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} \bullet \underbrace{|\xi_i+\eta_i|}_\text{Apply Triangle Inequality} \\ \Rightarrow \displaystyle\sum\limits_{i=1}^\infty{\omega_i}^p \leq \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1}(|\xi_i|+|\eta_i|) \\ \Rightarrow \displaystyle\sum\limits_{i=1}^\infty{\omega_i}^p \leq \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} |\xi_i| + \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} |\eta_i| \\ \label{eq:minkowski-separated-summed-inequality} \end{equation}\]

Apply Hölder’s Inequality \(\eqref{eq:holders-inequality}\) to each term on the RHS individually in \(\eqref{eq:minkowski-separated-summed-inequality}\), we have:

\[\displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} |\xi_i| \leq \displaystyle\sum\limits_{i=1}^\infty|\omega^{p-1} \xi_i| \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{\left({|\omega_i|}^{p-1}\right)}^q\right]}^\frac{1}{q} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\xi_i|}^p\right]}^\frac{1}{p} \\ \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} |\xi_i| \leq \displaystyle\sum\limits_{i=1}^\infty|\omega^{p-1} \xi_i| \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{\left({|\omega_i|}^{p-1}\right)}^q\right]}^\frac{1}{q} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\eta_i|}^p\right]}^\frac{1}{p}\]

Note that since \(p\) and \(q\) are conjugate exponents, we can write:

\[p=pq-q\]

Then the above inequalities simplify to:

\[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} |\xi_i| \leq \displaystyle\sum\limits_{i=1}^\infty|\omega^{p-1} \xi_i| \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{|\omega_i|}^p\right]}^\frac{1}{q} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\xi_i|}^p\right]}^\frac{1}{p} \label{eq:minkowski-holder-inequality-1} \end{equation}\] \[\begin{equation} \displaystyle\sum\limits_{i=1}^\infty\omega^{p-1} |\xi_i| \leq \displaystyle\sum\limits_{i=1}^\infty|\omega^{p-1} \xi_i| \leq {\left[\displaystyle\sum\limits_{i=1}^\infty|{\omega_i|}^p\right]}^\frac{1}{q} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\eta_i|}^p\right]}^\frac{1}{p} \label{eq:minkowski-holder-inequality-2} \end{equation}\]

Applying \(\eqref{eq:minkowski-holder-inequality-1}\) and \(\eqref{eq:minkowski-holder-inequality-2}\) to \(\eqref{eq:minkowski-separated-summed-inequality}\), we get:

\[\displaystyle\sum\limits_{i=1}^\infty{\omega_i}^p \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{|\omega_i|}^p\right]}^\frac{1}{q} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\xi_i|}^p\right]}^\frac{1}{p} + {\left[\displaystyle\sum\limits_{i=1}^\infty|{\omega_i|}^p\right]}^\frac{1}{q} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\eta_i|}^p\right]}^\frac{1}{p} \\ \displaystyle\sum\limits_{i=1}^\infty{\omega_i}^p \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{|\omega_i|}^p\right]}^\frac{1}{q} \left({\left[\displaystyle\sum\limits_{i=1}^\infty{|\xi_i|}^p\right]}^\frac{1}{p} + {\left[\displaystyle\sum\limits_{i=1}^\infty{|\eta_i|}^p\right]}^\frac{1}{p}\right) \\ {\left[\displaystyle\sum\limits_{i=1}^\infty{|\omega_i|}^p\right]}^{1-\frac{1}{q}} \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{|\xi_i|}^p\right]}^\frac{1}{p} + {\left[\displaystyle\sum\limits_{i=1}^\infty{|\eta_i|}^p\right]}^\frac{1}{p}\]

Again, noting from the conjugate exponent identity that \(1-\frac{1}{q}=\frac{1}{p}\), we get:

\[\begin{equation} {\left[\displaystyle\sum\limits_{i=1}^\infty{|\omega_i|}^p\right]}^\frac{1}{p} \leq {\left[\displaystyle\sum\limits_{i=1}^\infty{|\xi_i|}^p\right]}^\frac{1}{p} + {\left[\displaystyle\sum\limits_{i=1}^\infty{|\eta_i|}^p\right]}^\frac{1}{p} \label{eq:minkowski-inequality} \end{equation}\]

\(\eqref{eq:minkowski-inequality}\) is referred to as Minkowski’s Inequality.

---