General Proof Tactics for Real and Functional Analysis

Avishek Sen Gupta on 29 September 2021

---

This article represents a (very short) collection of my ongoing notes on proof tactics I’ve found useful when I’ve been stuck trying to solve proof exercises. I aim to continue documenting these in as much detail as possible. These are mostly aids while building intuition about how to prove something, and gradually should become part of one’s mental lexicon.

For now, here is a sketch of some of them.

• Work backwards from what the exercise requires you to prove.
• For Triangle Inequality proofs, look for opportunities to break up \(\vert x-y \vert\) into \(\vert x-z+z-y\vert \leq \vert x-z \vert + \vert z-y \vert\).
• Infimum (greatest lower bound) and supremum (least upper bound) of a set do not need to exist inside a set. Thus, the infimum/supremum of two sets can be the same without those sets intersecting. Use infinite sequences with infimum/supremum outside of the set to compare against a set (which contains the infimum/supremum) to prove infimums/supremums equal without set intersections.
• Use variations of \((x_k)=\sum\frac{1}{n}\) to demonstrate convergence of a sequence, but non-convergence of the corresponding series.
  • Use multiples of \((x_k)=\sum\frac{1}{n}\), like \((x_k)=\sum\frac{2^n}{n}\) and break each term into \(2^n\) number of \(\frac{1}{n}\)’s to demonstrate convergence of a sequence, but non-convergence of the corresponding series (or any multiple or power thereof).
• To rearrange terms in maximum expressions like \(\max(a+b, c+d)\), remember that: \(\max(a+b, c+d) \leq \max(a,c)+\max(b,d)\).
• To convert sums into products (or vice-versa), consider trying Hölder’s Inequality (or the simpler Cauchy-Schwarz Inequality) on sums of indexed products:
  \(x_1y_1+x_2y_2+...=\sum x_i y_i \leq {\left(\sum x_i^p\right)}^\frac{1}{p}{\left(\sum y_i^p\right)}^\frac{1}{p}\)
• If a constant term appears in the numerator of one term and the denominator of another, like \(\frac{x}{\lambda}+\lambda y\), try to select \(\lambda=\sqrt{\frac{x}{y}}\), so that you can get \(\sqrt{xy}+\sqrt{xy}=2\sqrt{xy}\).
• Use loose equalities, i.e., if \(x+y \leq z, x,y,z \geq 0\), then \(x \leq z\).

• Pathological Case where the Closure of an Open Ball is not the Closed Ball

  In a Discrete Metric Space, an open ball around an element \(x_0\) is \(d(x,x_0)<1\) is \(X=\{x_0\}\). Since there is no other \(x\) within every any neightbourhood of \(x_0\), which is not \(x_0\) itself, \(X=\{x0\}\) has no limit points. Then \(X=\{x_0\}\) vacuously contains all its limit points (of which there are actually none, so the empty set is the set of limit points). Thus, \(\bar{X}=\{x_0\}\) is its own closure.

  The closed ball around \(x_0\) is \(d(x,x_0)\leq 1\), which is everything, but it is not the same as \(\bar{X}=\{x_0\}\). The situation is shown below:

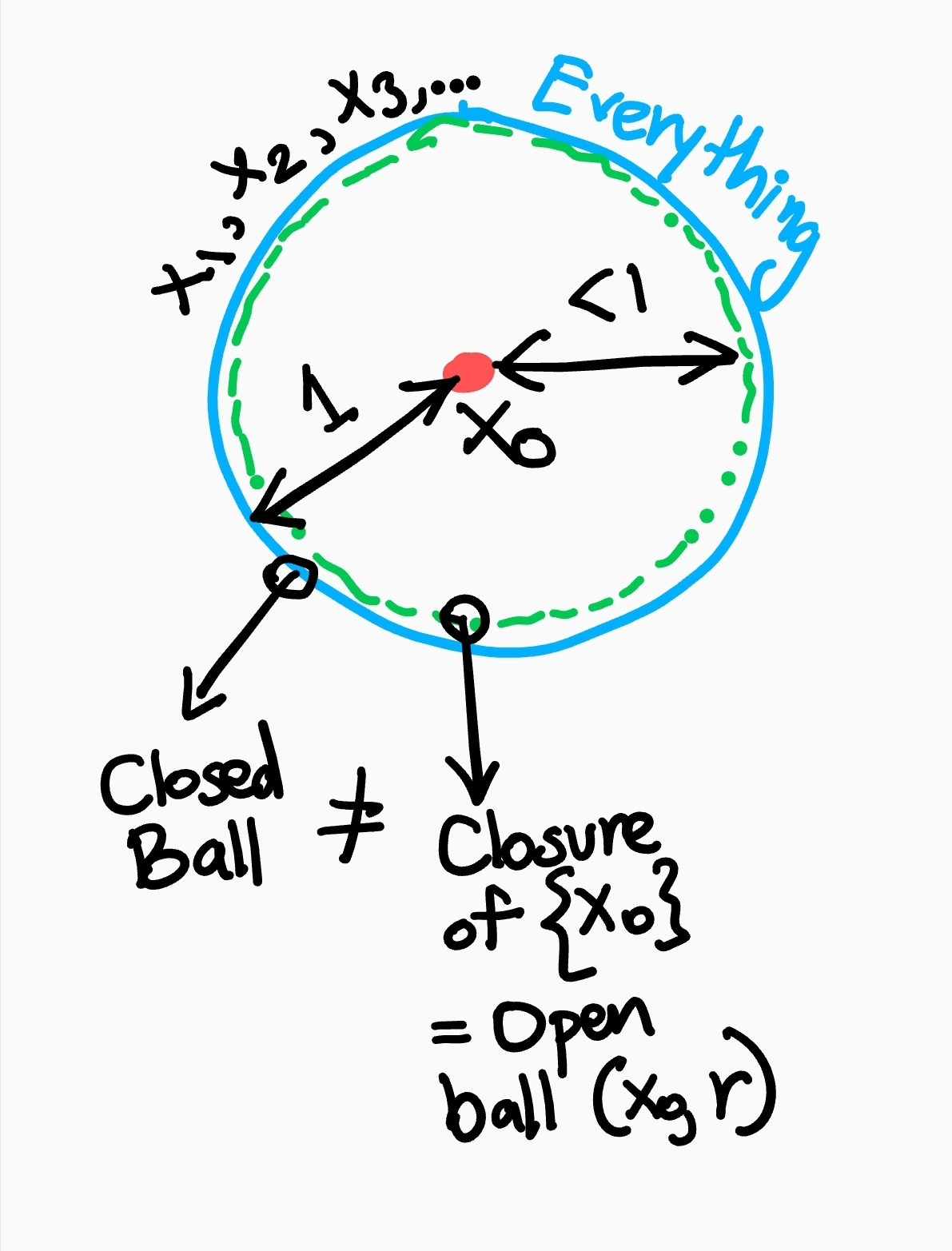
• To prove equality (between both numbers and sets), you can attempt to prove \(X=Y\) by proving \(X\geq Y, X\leq Y\) for numbers, and \(X \subseteq Y, X \supseteq Y\) for sets.

• Generate a discrete metric space from \(\mathbb{R}\) by assuming an interval \(X=(0,1)\), and converting each \(x\in X\) into its binary form, so that the representation looks like:

  \[x=\frac{x_1}{2^1}+\frac{x_1}{2^2}+\frac{x_1}{2^1}+\cdots\]
• Then \(d(x_1,x_2) : x_1,x_2 \in X = \begin{cases} 1 & \text{ if } x_1 \neq x_2 \\ 0 & \text{ if } x_1=x_2 \end{cases}\) This works when the distance metric is a “sup” metric like in \(l^\infty\) space. The set is also uncountable, since there are uncountable number of such sequences, and thus can be paired with arbitrary sets to disprove separability.
• To prove countability, utilise nearness of reals and rationals. Prove that a member of the countable set is close enough to the member of the “densee” set to prove separability.
• Proofs about closed sets can be simplified by considering known properties of open sets, and then taking their duals. The direct proof would involve proving properties about sequences which converge to limits, and assuming those limits are contained in closed sets.
• For establishing set membership relations, start with assuming one side (say, the left side), then breaking it down into cases. Then, expand membership into the right hand side.

• When trying to prove that a sequence is Cauchy, where the distance metric is bounded to some non-zero value, derive \(\epsilon\) by considering the diminishing distance between an arbitrary element and the limit. For example:

  \[d(x,y)=\vert \text{arc tan } x - \text{arc tan } y \vert\]

  Then we note that \(\text{arc tan } x \rightarrow \frac{\pi}{2}\) as \(x \rightarrow \infty\). Then \(\vert \text{arc tan } x - \frac{\pi}{2} \vert < \frac{\epsilon}{2}\). Then use this to prove the Cauchy criterion using the Triangle Inequality. That is:

  \[d(x_m,x_n) \leq d(x_m,x) + d(x,x_n) = \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon\]
• Note on Terminology: Instead of saying “\(\infty\) does not exist in a set”, say “no element in the set exists which satisfies the condition X”.
• An infinite series tends to zero the further out you start a subsequence.

---