Functional Analysis Exercises 5 : Completeness Proofs

Avishek Sen Gupta on 16 October 2021

---

This post lists solutions to the exercises in the Completeness Proofs section 1.5 of Erwin Kreyszig’s Introductory Functional Analysis with Applications. This is a work in progress, and proofs may be refined over time.

1.5.1 Let \(a,b \in \mathbb{R}\) and \(a<b\). Show that the open interval \((a,b)\) is an incomplete subspace of \(\mathbb{R}\), whereas the closed interval \([a, b]\) is complete.

Proof:

\((a,b)\) is not a closed set, since the limits of Cauchy sequences which converge to \(a\) and \(b\) are not contained in \((a,b)\). Thus \((a,b)\) is not complete.

\([a,b]\) is a closed set since it contains the limits of all the Cauchy sequences which converge, including \(a\) and \(b\). Thus, \([a.b]\) is a complete metric space.

\[\blacksquare\]

---

1.5.2 Let \(X\) be the space of all ordered n-tuples \(x = (\xi_1, \cdots, \xi_n)\) of real numbers and \(d(x,y)=\max_j \vert \xi_j-\eta_j\vert\) where \(y=(\eta_j)\). Show that \((X,d)\) is complete.

Proof:

Consider a Cauchy sequence of ordered n-tuples \((\xi^m) \in X\). By the Cauchy criterion, we have:

\[d(\xi^m, \xi^n)=\max|\xi^m_j - \xi^n_j|<\epsilon\]

This implies that \(\vert\xi^m_j - \xi^n_j\vert < \epsilon\).
For a fixed \(j\), we have a sequence of reals \(\xi^1_j, \xi^2_j, \cdots\) which is then a Cauchy sequence, and because of the completeness of \(\mathbb{R}\), this sequence converges to \(L_j \in \mathbb{R}\).

Then, we have for any \(m,j\), \(\vert\xi^m_j - L_j\vert < \epsilon\). It follows then that \(\max\vert\xi^m_j - L_j\vert < \epsilon\). This implies that the n-tuple formed by \((L)=L_1,L_2,\cdots,L_n\) is the limit of the Cauchy sequence \((\xi^m)\). Since \((\xi^m)\) was arbitrary, every Cauchy sequence in this space converges to a limit. Also, \(L \in X\), hence the limit is contained within this metric space.

Hence, this is a complete metric space.

\[\blacksquare\]

---

1.5.3 Let \(M \subset l^\infty\) be the subspace consisting of all sequences \(x = (\xi_j)\) with at most finitely many nonzero terms. Find a Cauchy sequence in \(M\) which does not converge in \(M\), so that \(M\) is not complete.

Proof:

\(l^\infty\) is the space of all bounded sequences. Let there be a Cauchy sequence \((x_n)\), where the \(n\)th sequence has \(n\) terms \(1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\cdots,\frac{1}{n}\).

This is a Cauchy sequence because for any \(m,n>N\), we have \(d(x^m,x^n)=\sup\vert x^m_j - x^n_j\vert=\displaystyle\frac{1}{\min(m,n)+1}\) and \(\min(m,n)\) can be made as large as possible to make \(\epsilon\) as small as possible (by the Archimedean Principle).

The limit of the Cauchy sequence is the infinite sequence \(1, \frac{1}{2}, \frac{1}{3}, \cdots\). Call it \(x\).

The distance between any \((x^n)\) and \(x\) will be \(\frac{1}{n+1}\). However, \(x\) is not contained in \(M\), since \(x\) does not have finitely many nonzero terms.

Thus, \(M \subset l^\infty\) is not a complete subset.

\[\blacksquare\]

---

1.5.4 Show that \(M\) in Prob. 3 is not complete by applying Theorem 1.4-7.

Proof:

The limit of the Cauchy sequence in \(M\) described in the previous problem, does not belong to \(M\), thus \(M\) is not a closed subset, and is thus not complete.

\[\blacksquare\]

---

1.5.5 Show that the set \(X\) of all integers with metric \(d\) defined by \(d(m,n) = \vert m-n\vert\) is a complete metric space.

Proof:

The only possible Cauchy sequences in this set are the ones ultimately yielding to the subsequence \(a,a,a,\cdots, a \in \mathbb{Z}\), because only then will the Cauchy criterion of \(d(x_m,x_n)<\epsilon, m,n>N\) hold.

Thus, every Cauchy sequence in this set has as its limit \(x \in \mathbb{Z}\). Thus, the set of all integers contains the limits of all its Cauchy sequences, and is thus a complete metric space.

\[\blacksquare\]

---

1.5.6 Show that the set of all real numbers constitutes an incomplete metric space if we choose \(d(x,y) = \vert \text{arc tan } x - \text{arc tan } y \vert\).

Proof:

Note that \(\text{arc tan }_{n\rightarrow\infty} n=\frac{\pi}{2}\).

We need to find a Cauchy sequence which has a limit not contained in \(\mathbb{R}\).

Assume \((x_n)=n\) We note that \(\text{arc tan } x \rightarrow \frac{\pi}{2}\) as \(x \rightarrow \infty\). Then \(\vert \text{arc tan } x - \frac{\pi}{2} \vert < \frac{\epsilon}{2}\). Then, we use this to prove that \((x_n)\) is Cauchy using the Triangle Inequality. That is:

\[d(x_m,x_n) \leq d(x_m,x) + d(x,x_n) = \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon\]

Then \((x_n)\) has a limit at \(\infty\). However, \(\mathbb{R}\) does not contain \(\infty\). Thus, this set if an incomplete metric space.

\[\blacksquare\]

---

1.5.7 Let \(X\) be the set of all positive integers and \(d(m,n)=\vert m^{-1}-n^{-1}\vert\). Show that \((X,d)\) is not complete.

Proof:

Let there be a sequence \((x_n)=n\). The distance \(d(x_n,x)=\vert \frac{1}{x_n} - \frac{1}{x} \vert\) as \(x \rightarrow \infty\) approaches \(\frac{1}{n}\) which can be made as small as needed by choosing a large enough \(n\). Thus we have:

\[d(x_n,x)=\vert \frac{1}{x_n} - \frac{1}{x} \vert < \epsilon\]

Then, by the Triangle Inequality, we have:

\[d(x_m,x_n) \leq d(x_m,x) + d(x,x_n) < \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon\]

Hence \((x_n)\) is Cauchy. However, this Cauchy does not converge in \(\mathbb{Z}_+\), because there is no element in the set where \(\frac{1}{x_m}=0\).

\[\blacksquare\]

---

1.5.8 (Space \(C[a, b]\)) Show that the subspace \(Y \subset C[a,b]\) consisting of all \(x \in C[a, b]\) such that \(x(a) = x(b)\) is complete.

Proof:

The distance metric on \(C[a.b]\) is defined as: \(d(f_1,f_2)=\sup\vert f_1(x), f_2(x)\vert\). We assume a Cauchy sequence of functions \((f_n)=f_1,f_2,f_3,\cdots\).

We have, by the Cauchy criterion:

\[d(f_m(x),f_n(x))<\epsilon \\ \Rightarrow \sup |f_m(x) - f_n(x)| < \epsilon \\ \Rightarrow |f_m(x) - f_n(x)| < \epsilon\]

Fix \(x=t\) such that \(f_1(t), f_2(t), \cdots\) forms a Cauchy sequence in \(\mathbb{R}\) since \(\vert f_m(t) - f_n(t) \vert < \epsilon\). Since \(\mathbb{R}\) is complete, this sequence also converges to a real number \(f_L(t)\).

Since \(t\) is arbitrary, all the limits of all \(t \in [a,b]\) form the values of a limit function; call it \(f_L(x)\).

Since this limit function exists, we have:

\[d(f_n(x),d_L(x))<\epsilon\]

Since we know that \(d(f_n(a), f_n(b))=0\), the above reduces to:

\[d(f_L(a), f_L(b)) \leq d(f_L(a), f_n(a)) + d(f_n(a), f_n(b)) + d(f_n(b),f_L(b)) \\ \Rightarrow d(f_L(a), f_L(b)) \leq \epsilon + 0 + \epsilon = 2 \epsilon\]

Since \(d(f_L(a), f_L(b))<2 \epsilon\) for all \(\epsilon>0\), it follows that \(d(f_L(a), f_L(b))=0\). Thus \(f_L\) is contained in the set of all \(x \in C[a, b]\) such that \(x(a) = x(b)\) is complete.

Hence this subset is complete.

\[\blacksquare\]

---

1.5.9 In 1.5-5 we referred to the following theorem of calculus. If a sequence \((x_m)\) of continuous functions on \([a,b]\) converges on \([a,b]\) and the convergence is uniform on \([a,b]\), then the limit function \(x\) is continuous on \([a,b]\). Prove this theorem.

Proof:

A sequence of functions \((f_n)=f_1,f_2,\cdots\) is uniformly convergent onto a limit function \(f\) if \(\forall \epsilon>0, \exists N\), such that \(\vert f_n(x)-f(x) \vert < \epsilon\) for all \(x\) and \(n>N\).

A function is continuous at a point \(x_0\) if \(\forall \epsilon>0, \exists \delta>0\) such that \(\vert x-x_0 \vert <\delta \Rightarrow \vert f(x)- f(x_0)\vert < \epsilon\).

Choose a function \(f_n\) where \(n>N\). Fix a point \(x_0\). Then, because of uniform convergence, we have:

\[d[f(x_0),f_n(x_0)]<\epsilon \\ d[f_n(x),f(x)]<\epsilon\]

Since \(f_n\) is continuous, it is also continuous at \(x_0\), pick an \(\epsilon>0\) such that \(d[f_n(x), f_n(x_0)]<\epsilon\).

Then, by the Triangle Inequality, we have:

\[d[f(x),f(x_0)] \leq d[f(x),f_n(x)] + d[f_n(x),f_n(x_0)] + d[f_n(x_0),f(x_0)] \\ \Rightarrow d[f(x),f(x_0)] < \epsilon + \epsilon + \epsilon = 3 \epsilon\]

This shows that the limit function \(f\) is also continuous.

\[\blacksquare\]

---

1.5.10 (Discrete metric) Show that a discrete metric space (cf. 1.1-8) is complete.

Proof: The discrete metric is defined as:

\[d(x,y)=\begin{cases} 0 & \text{if } x=y \\ 1 & \text{if } x \neq y \end{cases}\]

The only Cauchy sequences in \(X\) with this metric are those which yield to subsequences \(a,a,a,\cdots\). The limit of such a Cauchy sequence is \(a \in X\). Thus the limit exists and is contained by the set \(X\).

\[\blacksquare\]

---

1.5.11 (Space s) Show that in the space \(s\) (cf. 1.2-1) we have \(x_n \rightarrow x\) if and only if \(\xi^{(n)}_j \rightarrow \xi_j\) for all \(j = 1, 2, \cdots\) , where \(x_n=(\xi^{(n)}_j)\) and \(x=(\xi_j)\).

Proof:

The space \(s\) consists of all bounded and unbounded sequences with the metric:

\[d(x,y)=\displaystyle\sum\frac{1}{2^i}\frac{|x_i-y_i|}{1+|x_i-y_i|}\]

Assume \(x_n \rightarrow x\), so that \(d(\xi^n,\xi)<\epsilon/2\). Then, by the Triangle Inequality, we have:

\[d(\xi^m,\xi^n) \leq d(\xi^m,\xi) + d(\xi, \xi^n) < \epsilon/2 + \epsilon/2 = \epsilon\]

Thus, the Cauchy criterion also holds, so that: \(d(\xi^m,\xi^n)=\displaystyle\sum\frac{1}{2^j} \frac{|\xi^m_j-\xi^n_j|}{1+|\xi^m_j-\xi^n_j|} < \epsilon\)

Denote \(D_j=\vert\xi^m_j-\xi_j\vert\) for simplicity, so that we get:

We also note that \(\displaystyle\sum\frac{1}{2^j}=1\), so that we can write the following: \(\displaystyle\sum\frac{1}{2^j} \frac{D_j}{1+D_j} < \epsilon\sum\frac{1}{2^j} \\ \Rightarrow \displaystyle\sum\frac{1}{2^j} \frac{D_j}{1+D_j} < \sum\frac{\epsilon}{2^j}\)

Comparing term by term, we can say that:

\[\frac{D_j}{1+D_j}<\epsilon \\ \Rightarrow D_j<\epsilon(1+D_j) \\ \Rightarrow D_j(1-\epsilon)<\epsilon \\ \Rightarrow D_j<\frac{\epsilon}{1-\epsilon}\]

Note that \(\epsilon<1\) simply because \(\frac{D_j}{1+D_j}<1\) and \(\frac{1}{2^j}<1\). Setting \(\epsilon=\frac{1}{k}\), we get:

\[\frac{\epsilon}{1-\epsilon}=\frac{\frac{1}{n}}{1-\frac{1}{n}} = \frac{1}{n-1}\]

Thus, \(D_j\) can be made as small as needed by choosing a large \(n\), i.e., small \(\epsilon\), i.e.:

\[\vert\xi^m_j-\xi\vert < \epsilon_0\]

This implies that, for an arbitrary \(j\):

\[\xi^{(n)}_j \rightarrow \xi_j\] \[\blacksquare\]

Conversely, assume that \(\xi^{(n)}_j \rightarrow \xi_j\) for \(j=1,2,\cdots\).

This implies that:

\[\vert\xi^m_j-\xi_j\vert < \epsilon_0\]

Assume there is a sequence \(\xi_1, \xi_j, \cdots\).

We can see that:

\[\frac{|\xi^m_j-\xi_j|}{1+|\xi^m_j-\xi_j|}<|\xi^m_j-\xi_j|<\epsilon<1\]

Multiplying both sides by \(\frac{1}{2^n}\), we get:

\[\frac{1}{2^j}\frac{|\xi^m_j-\xi_j|}{1+|\xi^m_j-\xi_j|}<\frac{1}{2^j} \epsilon\]

Summing to \(\infty\), we get:

\[\sum\frac{1}{2^j}\frac{|\xi^m_j-\xi_j|}{1+|\xi^m_j-\xi_j|}<\sum\frac{1}{2^j} \epsilon \\ \Rightarrow d(\xi^m,\xi) < \epsilon\sum\frac{1}{2^j} \\ \Rightarrow d(\xi^m,\xi) < \epsilon\]

This implies that:

\[\xi^m \rightarrow \xi\] \[\blacksquare\]

---

1.5.12 Using Prob. 11, show that the sequence space \(s\) in 1.2-1 is complete.

Proof:

Assume a Cauchy sequence in the space \(s\). Since it is a Cauchy sequence, we have:

\[d(\xi^m,\xi_n) < \epsilon\]

By the previous problem, this would imply that

\[\vert\xi^m_j-\xi^n_j\vert < \epsilon\]

For a fixed \(j\), we thus have a Cauchy sequence of reals. Since \(\mathbb{R}\) is complete, this sequence converges so that \(\xi^n_j \rightarrow \xi_j\).

By the previous problem, this implies that the Cauchy sequence in the space \(s\) converges to a limit \(\xi\). Moreover, \(\xi \in s\). Hence \(s\) is a complete metric space.

\[\blacksquare\]

---

1.5.13 Show that in 1.5-9, another Cauchy sequence is \((x_n)\), where \(x_n(t)=n \text{ if } 0 \leq t \leq n^{-2}\) and \(x_n(t)=t^{-\frac{1}{2}} \text{ if } n^{-2} \leq t \leq 1\).

Proof:

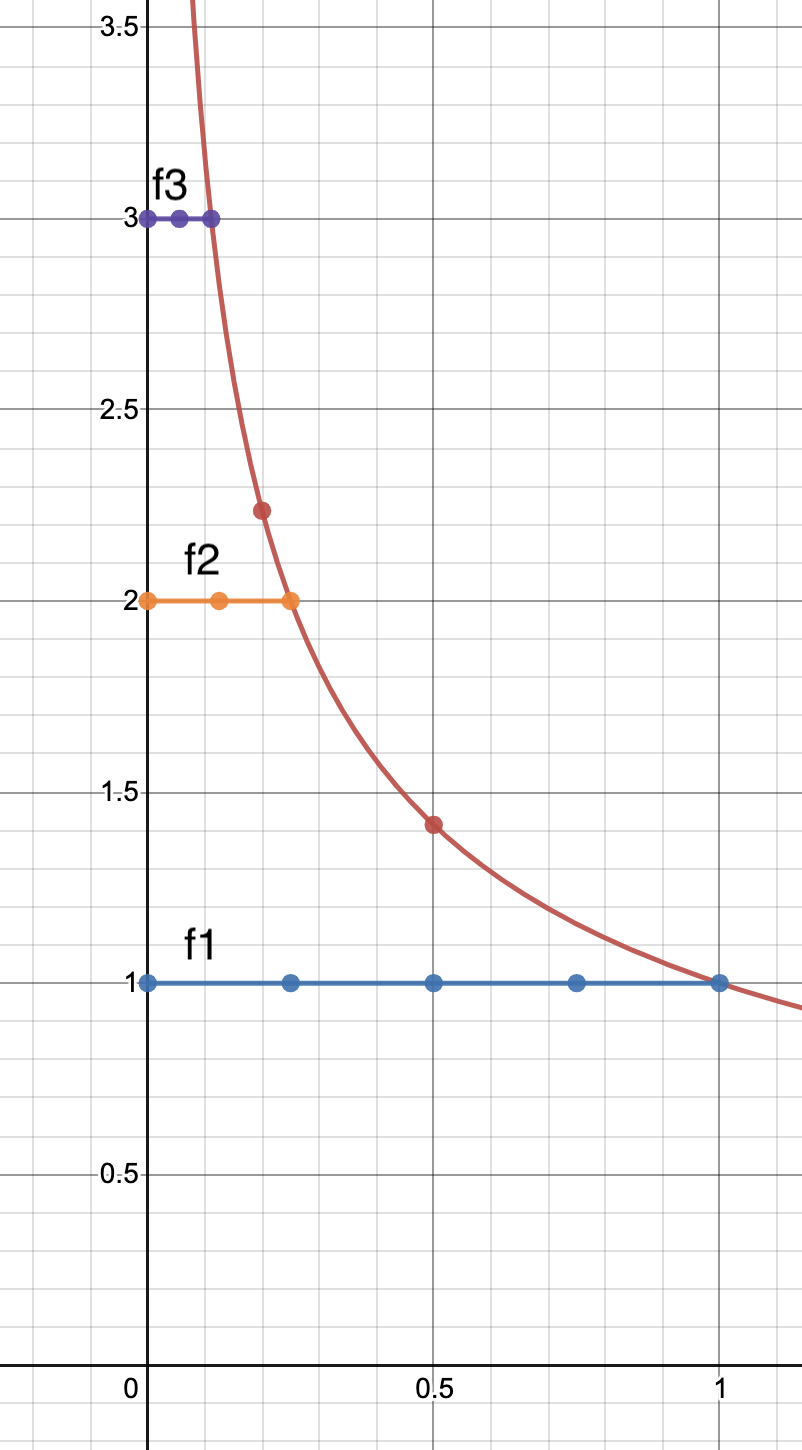
We prove that this sequence is Cauchy. The distance metric is defined as:

\[d(x,y)=\int\limits_0^1 |x(t) - y(t)| dt\] \[d(x_m,x_n)=\int\limits_0^1 |x_m(t) - x_n(t)| dt \\ = \int\limits_0^{\frac{1}{n^2}} |x_m(t) - x_n(t)| dt + \int\limits_{\frac{1}{n^2}}^{\frac{1}{m^2}} |x_m(t) - x_n(t)| dt + \int\limits_{\frac{1}{m^2}}^1 |x_m(t) - x_n(t)| dt \\ = \int\limits_0^{\frac{1}{n^2}} |n-m| dt + \int\limits_{\frac{1}{n^2}}^{\frac{1}{m^2}} |m-\frac{1}{\sqrt t}| dt + \int\limits_{\frac{1}{m^2}}^1 |\frac{1}{\sqrt t}-\frac{1}{\sqrt t}| dt \\ = \int\limits_0^{\frac{1}{n^2}} (n-m) dt + \int\limits_{\frac{1}{n^2}}^{\frac{1}{m^2}} (\frac{1}{\sqrt t}-m) dt + \int\limits_{\frac{1}{m^2}}^1 |\frac{1}{\sqrt t}-\frac{1}{\sqrt t}| dt \\\]

Note above that for the middle term \(\frac{1}{\sqrt t}>m\), thus the terms are flipped.

Assuming \(m<n\), we get:

\[\require{cancel} (n-m)(\frac{1}{n^2} - 0) + m(\frac{1}{n^2} - \frac{1}{m^2}) - (\frac{2}{n} - \frac{2}{m}) + 0 \\ = \frac{1}{n} - \cancel{\frac{m}{n^2}} + \cancel{\frac{m}{n^2}} -\frac{1}{m} - \frac{2}{n} + \frac{2}{m} \\ = \frac{1}{m} - \frac{1}{n}=\frac{n-m}{mn}\]

Assume you keep \(n-m=K\), then you can make \(d(x_m, x_n)<\epsilon\) by choosing suitable \(m,n\) so that the product \(mn\) is as large as needed.

Thus \((x_n)\) is a Cauchy sequence.

\[\blacksquare\]

---

1.5.14 Show that the Cauchy sequence in Prob. 13 does not converge.

Proof:

Assume that the limit of \(x_n\) exists, and is \(x(t)\). Thus, as \(n \rightarrow \infty\), \(d(x_m(t),x(t)) \rightarrow 0\), implying that the integral above approaches zero. Since, all the integrands are positive, each of them should individually approach zero.

Then, we get, in the limit of \(n \rightarrow \infty\):

\[\int\limits_0^0 |n-x(t)| dt + \int\limits_0^{\frac{1}{m^2}} |m-x(t)| dt + \int\limits_{\frac{1}{m^2}}^1 |\frac{1}{\sqrt t}-x(t)| dt \\\]

The three terms above should individually go to zero. Thus, the third term implies that \(x(t)=\frac{1}{\sqrt t}\).

\(x(t)\) should be in the space of continuous functions. However \(x(t)=\frac{1}{\sqrt t}\) is not defined for \(t=0\). Thus, \(x(t)\) is not continuous, and this Cauchy sequence in \(C[0,1]\) does not converge.

\[\blacksquare\]

---

1.5.15 Let \(X\) be the metric space of all real sequences \(x=(\xi_j)\) each of which has only finitely many nonzero terms, and \(d(x,y)=\displaystyle\sum \vert \xi_j - \eta_j \vert\), where \(y = (\eta_j)\). Note that this is a finite sum but the number of terms depends on \(x\) and \(y\). Show that \((x_n)\) with \(x_n = (\xi^{(n)}_j)\),

\(\xi^{(n)}_j=j^{-2}\) for \(j=1,\cdots,n\) and \(\xi^{(n)}_j=0\) for \(j>n\)

is Cauchy but does not converge.

Proof:

Consider the space of sequences \((x_n)=\frac{1}{1},\frac{1}{2^2},\frac{1}{3^2},\cdots,\frac{1}{n^2},0,0,\cdots\).

We have \(d(x_m,x_n)=\displaystyle\sum\limits_{j=m+1}^n \frac{1}{j^2}\). Since \(\displaystyle\sum\limits_{j=1}^\infty \frac{1}{j^2}\) is bounded, \(\displaystyle\sum\limits_{j=n}^\infty \frac{1}{j^2}\) can be made as small as needed, by choosing a large \(m\), thus we have:

\[\displaystyle\sum\limits_{j=m+1}^n \frac{1}{j^2}<\displaystyle\sum\limits_{j=m+1}^\infty \frac{1}{j^2}<\epsilon.\]

Thus, this sequence is Cauchy.

Assume a limit exists, then \(d(x_n,x) \rightarrow 0\) as \(n \rightarrow \infty\).

Then \(\require{cancel} d(x_n,x)=\displaystyle\sum\limits_{j=n+1}^\infty \frac{1}{j^2} \cancel\rightarrow 0\)

which is a contradiction. Thus, this limit does not exist in \(X\), and thus \(X\) is not a complete metric space.

\[\blacksquare\]

---