Total Internal Reflection
Technology and Art
Code
Contact
Transformers using PyTorch : Worklog Part 1
It may seem strange that I’m jumping from implementing a simple neural network into Transformers. I will return to building up the foundations of neural networks soon enough: for the moment, let’s build a Transformer using PyTorch.
The original paper is Attention is All You Need. However, there are several excellent guides to understanding the original Transformers architecture; I will use The Illustrated Transformer by Jay Alammar to guide this implementation; many of the diagrams of the Transformer internals are gratefully borrowed from his site.
Part 2 of this series of posts on Transformer is also available now.
As is obligatory, we reproduce the original Transformer architecture before diving into the depths of its implementation.
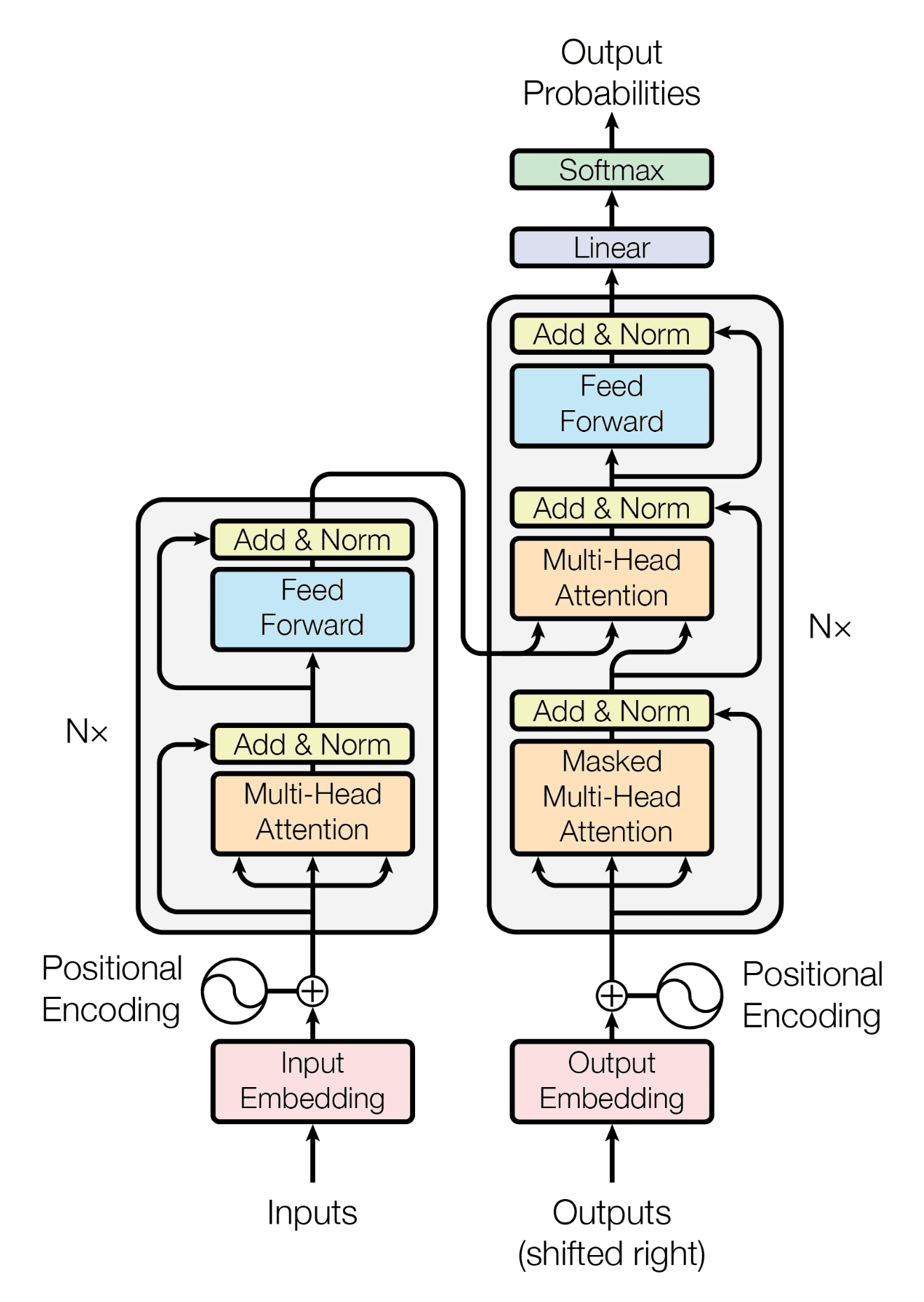
One thing about this guide is that it does not start with a polished walkthrough of the finished code. Rather, we build it in stages, experimenting with PyTorch API’s, adding/modifying/deleting code as I go along. The idea is two-fold: one, to give you a sense of what goes behind implementing a paper incrementally, and second, to demonstrate that progress while writing code is not necessarily linear.
Also, apart from some stock functionality like Linear and LayerNorm, we won’t be using any Transformer-specific layers available in PyTorch, like MultiheadAttention. This is so we can gain a better understanding of the attention mechanism by building it ourselves.
We will start with following the simplified block diagram as is presented on the site.
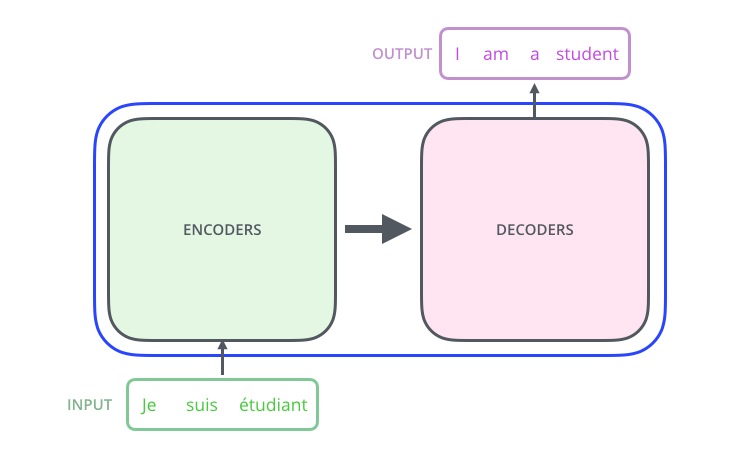
We will start without any PyTorch dependencies, and almost blindly build an object model based on this diagram. The paper says that there are 6 encoders stacked on top of each other, so we will build a simple linked encoder graph. Most of this code will be probably thrown away later, but at this point we are feeling out the structure of the solution without worrying too much about the details: experimenting with the details will come later. Here’s the code:
def encoder_stack(EncoderCtor, num_encoders):
if (num_encoders == 0):
return None
return EncoderCtor(encoder_stack(EncoderCtor, num_encoders - 1))
class EncoderCtor:
def __init__(self, next_encoder):
self.next = next_encoder
start_encoder = encoder_stack(EncoderCtor, 6)
print(start_encoder)
Replicating the decoder block diagram is almost as easy: simply steal code from the encoder. We will probably not get to the decoder for a while, but this is a exercise to get a lay of the land before getting lost in the weeds.
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class EncoderCtor:
def __init__(self, next):
self.next = next
class DecoderCtor:
def __init__(self, next):
self.next = next
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
print(start_encoder)
At this point, we will want to start taking a peek at the insides of the encoder and the decoder. The breakdown looks like as below:
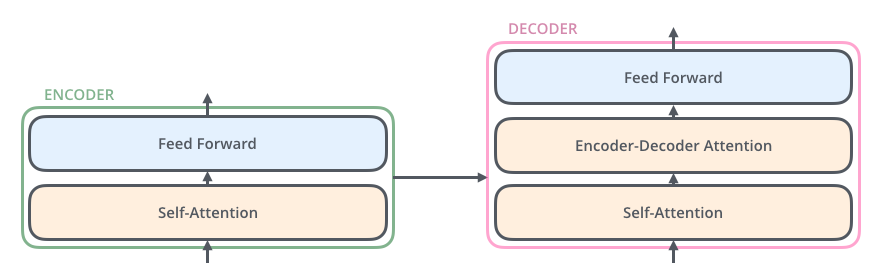
We want to build these blocks, but building the Self-Attention layer is going to take a while, and we don’t want to wait to build out the scaffolding. Thus, what we will do is build all these blocks and assume they are all vanilla Feedforward neural networks. It does not matter that this is not the actual picture: we’re mostly interested in filling the blanks. We can always go back and replace parts as we see fit.
Thus, even the Self-Attention layers are also represented as Feedforward neural networks, and the code is as below:
import torch.nn as nn
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class EncoderCtor(nn.Module):
def __init__(self, next):
super(EncoderCtor, self).__init__()
self.next = next
self_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, feedforward_layer)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
print(start_encoder)
To be honest, a lot of this is pretty dirty code; there are magic numbers, most of the object variables are not used. That’s alright. This is also the first time we start including PyTorch dependencies.
We’ve created a Sequential stack to house our layers, but there is not much to say about it, since it is essentially a placeholder for the real layers to be built in and incorporated.
Our initial aim is similar to the mathematics problems on dimensional analysis we used to solve in school: namely, we want to get the dimensions of our inputs and outputs correct and parameterisable. We will start with one word, and midway, scale to supporting multiple words.
Introducing the Query-Key-Value triad function
This step is pretty simple: we will introduce the function which returns us the Key-Query-Value triad for a given word. Remember that we are not worried about the actual calculations right now; we will only worry ourselves about getting the dimensions right. Since the original paper mentions scaling the input to 64 dimensions, our function will simply return three 64-dimensional tensors filled with ones.
import torch
import torch.nn as nn
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class EncoderCtor(nn.Module):
def __init__(self, next):
super(EncoderCtor, self).__init__()
self.next = next
self_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, feedforward_layer)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
def qkv(input):
return (torch.ones(64), torch.ones(64), torch.ones(64))
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
print(start_encoder)
Applying the Query-Key-Value function to a single word
We can immediately move to the next logical step: actually multiplying our 512-dimensional input by \(W_Q\), \(W_K\) and \(W_V\) matrices. Remember we still want to get out three 64-dimensional vectors, thus the sizes of these matrices will be \(512 \times 64\). This is also when we actually multiply the input with these vectors in our qkv() function.
import torch
import torch.nn as nn
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class EncoderCtor(nn.Module):
def __init__(self, next):
super(EncoderCtor, self).__init__()
self.next = next
self_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, feedforward_layer)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.ones([512, 64])
W_K = torch.ones([512, 64])
W_V = torch.ones([512, 64])
def qkv(input):
return (torch.matmul(input, W_Q), torch.matmul(input, W_K), torch.matmul(input, W_V))
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
print(start_encoder)
print(qkv(torch.ones(512)))
Building the Attention Score for a single word
At this point, we are ready have the three vectors \(Q\), \(K\), and \(V\). We are about to implement part of the following calculation, except that it is for a single word:
\[Z = \displaystyle\text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) \times V\]The single word version of the above calculation for the \(i\)-th word can be written as:
\[Z_i = \displaystyle\sum_{j=1}^N \text{Softmax} \left(\frac {Q_i K_j}{\sqrt{d_K}}\right) V_j\]In the current case, we only have one word in total, so the above simply reduces to:
\[Z_1 = \displaystyle\text{Softmax} \left(\frac {Q_1 K_1}{\sqrt{d_K}}\right) V_1\]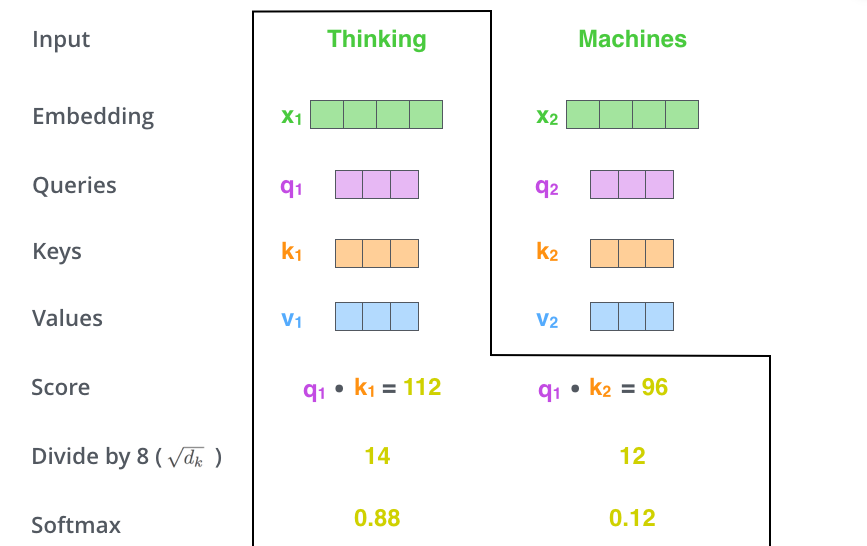
import torch
import torch.nn as nn
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class EncoderCtor(nn.Module):
def __init__(self, next):
super(EncoderCtor, self).__init__()
self.next = next
self_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, feedforward_layer)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.ones([512, 64])
W_K = torch.ones([512, 64])
W_V = torch.ones([512, 64])
def qkv(input):
return torch.matmul(input, W_Q), torch.matmul(input, W_K), torch.matmul(input, W_V)
def attention_score(qkv):
return torch.dot(qkv[0], qkv[1]) / 8
def softmax_scores(scores):
softmax = torch.nn.Softmax(dim=0)
return softmax(scores)
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
word = torch.ones(512)
test_qkv_1 = qkv(word)
test_qkv_2 = qkv(word)
test_qkv_3 = qkv(word)
attention_scores = torch.tensor([attention_score(test_qkv_1),
attention_score(test_qkv_2),
attention_score(test_qkv_3), ])
scores = softmax_scores(attention_scores)
print(test_qkv_1[2] * scores[0])
print(test_qkv_2[2] * scores[1])
print(test_qkv_3[2] * scores[2])
Building the Attention Scores for multiple words
Now, we are ready to go a little more production-strength. Instead of dealing with individual words, we will stack them in a \(N \times 512\) tensor (\(N\) being the number of words), and build the attention scores of all of these words, using the matrix version of the calculation, like we noted in the previous section. Specifically:
\[Z = \displaystyle\text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) \times V\]I think it is instructive to understand why this matrix multiplication works. To unpack this, let us discard the scaling factor (\(\sqrt{d_k}\)) and the Softmax function, leaving us with the core of the calculation:
\[Z = Q K^T V\]Let us take a concrete example of 2 words. Then, \(Q\), \(K\), and \(V\) are all \(2 \times 64\) tensors. Specifically, let us write:
\[Q = \begin{bmatrix} Q_1 \\ Q_2 \end{bmatrix} K = \begin{bmatrix} K_1 \\ K_2 \end{bmatrix} V = \begin{bmatrix} V_1 \\ V_2 \end{bmatrix}\]where \(Q_1\), \(Q_2\) (queries for the two words), \(K_1\), and \(K_2\) (keys for the two words), \(V_1\), and \(V_2\) (values for the two words)are 64-dimensional tensors. Then we have:
\[QK^T = \begin{bmatrix} Q_1 K_1 && Q_1 K_2 \\ Q_2 K_1 && Q_2 K_2 \\ \end{bmatrix}\]and then we have:
\[QK^T V = \begin{bmatrix} Q_1 K_1 && Q_1 K_2 \\ Q_2 K_1 && Q_2 K_2 \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix}\]We want to treat these product as the weighted combinations of the rows of \(V\), thus we get:
\[QK^T V = \begin{bmatrix} Q_1 K_1 V_1 + Q_1 K_2 V_2 \\ Q_2 K_1 V_1 + Q_2 K_2 V_2 \end{bmatrix} = \begin{bmatrix} \text{Attention Score of Word 1} \\ \text{Attention Score of Word 2} \\ \end{bmatrix}\]The first row is the (simplified) attention score of the first word, and the second one that of the second word. The scaling and the Softmax just gives us the linearly transformed version of the above.
import torch
import torch.nn as nn
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class EncoderCtor(nn.Module):
def __init__(self, next):
super(EncoderCtor, self).__init__()
self.next = next
self_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, feedforward_layer)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
word_width = 512
W_Q = torch.randn([word_width, 64]) / 100
W_K = torch.randn([word_width, 64]) / 100
W_V = torch.randn([word_width, 64]) / 100
def qkv(word):
return torch.matmul(word, W_Q), torch.matmul(word, W_K), torch.matmul(word, W_V)
def qkvs(words):
return torch.matmul(words, W_Q), torch.matmul(words, W_K), torch.matmul(words, W_V)
def attention_score(qkv):
return torch.dot(qkv[0], qkv[1]) / 8
softmax = torch.nn.Softmax(dim=1)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
def softmax_scores(scores):
softmax = torch.nn.Softmax(dim=0)
return softmax(scores)
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
word = torch.ones(word_width)
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words)
print(attention_scores(qkv_words))
attention_scores = torch.tensor([attention_score(test_qkv_1),
attention_score(test_qkv_2),
attention_score(test_qkv_3), ])
Encapsulating Attention Score calculation into a custom layer
We are well on our way to building out a functional (at least where input/output sizes are concerned) encoder layer. This step has some basic refactoring. Now that we know our calculations are ready, let us move into a custom SelfAttentionLayer.
import torch
import torch.nn as nn
softmax = torch.nn.Softmax(dim=1)
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class SelfAttentionLayer(nn.Module):
def __init__(self, w_q, w_k, w_v):
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words))
class EncoderCtor(nn.Module):
def __init__(self, next):
super(EncoderCtor, self).__init__()
self.next = next
self_attention_layer = SelfAttentionLayer(W_Q, W_K, W_V)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, feedforward_layer)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
word_width = 512
W_Q = torch.randn([word_width, 64]) / 100
W_K = torch.randn([word_width, 64]) / 100
W_V = torch.randn([word_width, 64]) / 100
def qkvs(words):
return torch.matmul(words, W_Q), torch.matmul(words, W_K), torch.matmul(words, W_V)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
word = torch.ones(word_width)
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words)
print(attention_scores(qkv_words))
print(SelfAttentionLayer(W_Q, W_K, W_V).forward(words))
Incorporating the Self Attention layer into the Encoder
The magic numbers are getting pretty ugly; let’s start moving them into variables for readability. This is also the point at which we build the multi-head attention block by running the input through eight attention blocks. Notice how much little of the original code we have really touched; that will be getting replaced very soon.
import torch
import torch.nn as nn
softmax = torch.nn.Softmax(dim=1)
num_heads = 8
word_width = 512
projection_width = 64
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class SelfAttentionLayer:
def __init__(self, w_q, w_k, w_v):
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words, self.w_q, self.w_k, self.w_v))
class EncoderCtor(nn.Module):
def __init__(self, w_o):
super(EncoderCtor, self).__init__()
self.w_o = w_o
self.attention_layers = list(map(lambda x: SelfAttentionLayer(W_Q, W_K, W_V), range(num_heads)))
self.feedforward_layer = nn.Linear(1, 1, bias=True)
def forward(self, x):
# Concatenating gives [num_words x num_heads * projection_width]
attention_vectors = list(map(lambda attention_layer: attention_layer.forward(x), self.attention_layers))
return torch.matmul(torch.cat(attention_vectors, dim=1), self.w_o)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.randn([word_width, projection_width]) / 100
W_K = torch.randn([word_width, projection_width]) / 100
W_V = torch.randn([word_width, projection_width]) / 100
W_O = torch.randn([num_heads * projection_width, word_width]) / 100
def qkvs(words, w_q, w_k, w_v):
return torch.matmul(words, w_q), torch.matmul(words, w_k), torch.matmul(words, w_v)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
word = torch.ones(word_width)
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words, W_Q, W_K, W_V)
# print(attention_scores(qkv_words))
# print(SelfAttentionLayer(W_Q, W_K, W_V).forward(words))
encoder = EncoderCtor(W_O)
encoder.eval()
print(encoder(words).shape)
Projecting the Attention Outputs back into original word width
We are mostly done with building the Attention part of the Encoder; we’d like to get started on the Feedforward Neural Network. However, to do that, the output of the Attention component needs to projected back into 512-dimensional space (the original word width). This is achieved by multiplying the output (\(N \times (64*8)\)) by \(W_O\) (\((64*8) \times 512\)).
At this point, we are ready to pass the output into the Feedforward neural network.
import torch
import torch.nn as nn
softmax = torch.nn.Softmax(dim=1)
num_heads = 8
word_width = 512
projection_width = 64
scale_factor = 100
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class SelfAttentionLayer:
def __init__(self, w_q, w_k, w_v):
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words, self.w_q, self.w_k, self.w_v))
class EncoderCtor(nn.Module):
def __init__(self, num_heads, w_o):
super(EncoderCtor, self).__init__()
self.w_o = w_o
self.attention_layers = list(map(lambda x: SelfAttentionLayer(W_Q, W_K, W_V), range(num_heads)))
self.feedforward_layer = nn.Linear(1, 1, bias=True)
def forward(self, x):
# Concatenating gives [num_words x num_heads * projection_width]
attention_vectors = list(map(lambda attention_layer: attention_layer.forward(x), self.attention_layers))
return torch.matmul(torch.cat(attention_vectors, dim=1), self.w_o)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.randn([word_width, projection_width]) / scale_factor
W_K = torch.randn([word_width, projection_width]) / scale_factor
W_V = torch.randn([word_width, projection_width]) / scale_factor
W_O = torch.randn([num_heads * projection_width, word_width]) / scale_factor
def qkvs(words, w_q, w_k, w_v):
return torch.matmul(words, w_q), torch.matmul(words, w_k), torch.matmul(words, w_v)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
start_encoder = coder_stack(EncoderCtor, 6)
start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
word = torch.ones(word_width)
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words, W_Q, W_K, W_V)
# print(attention_scores(qkv_words))
# print(SelfAttentionLayer(W_Q, W_K, W_V).forward(words))
encoder = EncoderCtor(num_heads, W_O)
encoder.eval()
print(encoder(words).shape)
Adding Feedforward Neural Network
We’d already built a FFNN in one of our first iterations; now we need to hook it up to the output of the Attention layer. Each word needs to be run through the same FFNN. Each word width is 512, thus the number of inputs to the FFNN is 512. The output needs to be of the same dimension. For this iteration, we will not worry about the ReLU and the hidden layer; a single layer will suffice to demonstrate that the Encoder in its current form can give a dimensionally-correct output.
import torch
import torch.nn as nn
softmax = torch.nn.Softmax(dim=1)
num_heads = 8
word_width = 512
projection_width = 64
scale_factor = 100
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class SelfAttentionLayer:
def __init__(self, w_q, w_k, w_v):
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words, self.w_q, self.w_k, self.w_v))
class EncoderCtor(nn.Module):
def __init__(self, num_heads, w_o, word_width):
super(EncoderCtor, self).__init__()
self.w_o = w_o
self.attention_layers = list(map(lambda x: SelfAttentionLayer(W_Q, W_K, W_V), range(num_heads)))
self.feedforward_layer = nn.Linear(word_width, word_width, bias=True)
def forward(self, x):
# Concatenating gives [num_words x num_heads * projection_width]
attention_vectors = list(map(lambda attention_layer: attention_layer.forward(x), self.attention_layers))
scaled_concatenated_attention_vectors = torch.matmul(torch.cat(attention_vectors, dim=1), self.w_o)
ffnn_outputs = list(map(lambda attention_vector: self.feedforward_layer(attention_vector), scaled_concatenated_attention_vectors))
return torch.stack(ffnn_outputs)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.randn([word_width, projection_width]) / scale_factor
W_K = torch.randn([word_width, projection_width]) / scale_factor
W_V = torch.randn([word_width, projection_width]) / scale_factor
W_O = torch.randn([num_heads * projection_width, word_width]) / scale_factor
def qkvs(words, w_q, w_k, w_v):
return torch.matmul(words, w_q), torch.matmul(words, w_k), torch.matmul(words, w_v)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
# start_encoder = coder_stack(EncoderCtor, 6)
# start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words, W_Q, W_K, W_V)
encoder = EncoderCtor(num_heads, W_O, word_width)
encoder.eval()
values = encoder(words)
print(values)
print(values.shape)
Fixing Feedforward Neural Network architecture
We’d like to now tune the FFNN architecture in line with the paper. The paper notes that there is one hidden layer consisting of 2048 units, followed by a ReLU layer. Thus, we have the following architecture:
- 512 outputs fully connected to 2048 units
- 2048 units passing their outputs through a ReLU layer
- ReLU layer fully connected to a layer of 512 units (remember, our output needs to be 512-dimensional)
This is described in the paper as:
\[FFN(x) = \text{max}(0,xW_1 + b_1) W_2 + b_2\]This neural network needs to be applied as many times as we have words. So if we have 4 words, our word matrix is represented as a \(4 \times 512\) matrix; and each row (of size 512) of this matrix needs to be passed into the FFNN. That’s 4 rows in this case.
The FFNN is wrapped in a Sequential module, and uses a Leaky ReLU.
import torch
import torch.nn as nn
softmax = torch.nn.Softmax(dim=1)
num_heads = 8
word_width = 512
projection_width = 64
scale_factor = 100
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class SelfAttentionLayer:
def __init__(self, w_q, w_k, w_v):
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words, self.w_q, self.w_k, self.w_v))
class EncoderCtor(nn.Module):
def __init__(self, num_heads, w_o, word_width):
super(EncoderCtor, self).__init__()
self.w_o = w_o
self.attention_layers = list(map(lambda x: SelfAttentionLayer(W_Q, W_K, W_V), range(num_heads)))
self.feedforward_layer = nn.Sequential(nn.Linear(word_width, 2048, bias=True), nn.LeakyReLU(), nn.Linear(2048, word_width, bias=True))
def forward(self, x):
# Concatenating gives [num_words x num_heads * projection_width]
attention_vectors = list(map(lambda attention_layer: attention_layer.forward(x), self.attention_layers))
scaled_concatenated_attention_vectors = torch.matmul(torch.cat(attention_vectors, dim=1), self.w_o)
ffnn_outputs = list(map(lambda attention_vector: self.feedforward_layer(attention_vector), scaled_concatenated_attention_vectors))
return torch.stack(ffnn_outputs)
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.randn([word_width, projection_width]) / scale_factor
W_K = torch.randn([word_width, projection_width]) / scale_factor
W_V = torch.randn([word_width, projection_width]) / scale_factor
W_O = torch.randn([num_heads * projection_width, word_width]) / scale_factor
def qkvs(words, w_q, w_k, w_v):
return torch.matmul(words, w_q), torch.matmul(words, w_k), torch.matmul(words, w_v)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
# start_encoder = coder_stack(EncoderCtor, 6)
# start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words, W_Q, W_K, W_V)
encoder = EncoderCtor(num_heads, W_O, word_width)
encoder.eval()
values = encoder(words)
print(values)
print(values.shape)
Adding Add-and-Norm Layer with Residual Connections
We still need to add the residual connections which are added and normed to the outputs of both the Multihead Attention block and the FFNN. This is simply a matter of element-wise adding of the input and passing the result through a LayerNorm layer.
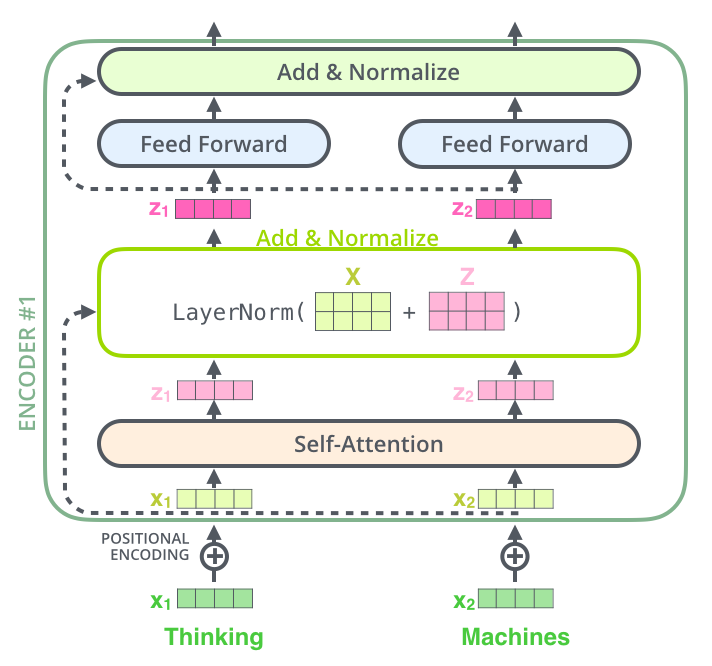
import torch
import torch.nn as nn
softmax = torch.nn.Softmax(dim=1)
num_heads = 8
word_width = 512
projection_width = 64
scale_factor = 100
def coder_stack(CoderCtor, num_encoders):
if (num_encoders == 0):
return None
return CoderCtor(coder_stack(CoderCtor, num_encoders - 1))
class SelfAttentionLayer:
def __init__(self, w_q, w_k, w_v):
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words, self.w_q, self.w_k, self.w_v))
class MultiheadedAttention(nn.Module):
def __init__(self, num_heads, w_o, word_width):
super(MultiheadedAttention, self).__init__()
self.w_o = w_o
self.attention_layers = list(map(lambda x: SelfAttentionLayer(W_Q, W_K, W_V), range(num_heads)))
def forward(self, x):
# Concatenating gives [num_words x num_heads * projection_width]
attention_vectors = list(map(lambda attention_layer: attention_layer.forward(x), self.attention_layers))
concatenated_attention_vectors = torch.cat(attention_vectors, dim=1)
scaled_concatenated_attention_vectors = torch.matmul(concatenated_attention_vectors, self.w_o)
return scaled_concatenated_attention_vectors
class EncoderCtor(nn.Module):
def __init__(self, num_heads, w_o, word_width):
super(EncoderCtor, self).__init__()
self.w_o = w_o
self.layer_norm = nn.LayerNorm(word_width)
self.multiheaded_attention_layer = MultiheadedAttention(num_heads, w_o, word_width)
self.feedforward_layer = nn.Sequential(nn.Linear(word_width, 2048, bias=True), nn.LeakyReLU(), nn.Linear(2048, word_width, bias=True))
def forward(self, x):
mh_output = self.multiheaded_attention_layer(x)
layer_normed_multihead = self.layer_norm(mh_output + x)
ffnn_outputs = torch.stack(list(map(lambda attention_vector: self.feedforward_layer(attention_vector), layer_normed_multihead)))
layer_normed_ffnn = self.layer_norm(ffnn_outputs + layer_normed_multihead)
return layer_normed_ffnn
class DecoderCtor(nn.Module):
def __init__(self, next):
super(DecoderCtor, self).__init__()
self_attention_layer = nn.Linear(1, 1, bias=True)
encoder_decoder_attention_layer = nn.Linear(1, 1, bias=True)
feedforward_layer = nn.Linear(1, 1, bias=True)
self.stack = nn.Sequential(self_attention_layer, encoder_decoder_attention_layer, feedforward_layer)
W_Q = torch.randn([word_width, projection_width]) / scale_factor
W_K = torch.randn([word_width, projection_width]) / scale_factor
W_V = torch.randn([word_width, projection_width]) / scale_factor
W_O = torch.randn([num_heads * projection_width, word_width]) / scale_factor
def qkvs(words, w_q, w_k, w_v):
return torch.matmul(words, w_q), torch.matmul(words, w_k), torch.matmul(words, w_v)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / 8.), qkvs[2])
# start_encoder = coder_stack(EncoderCtor, 6)
# start_decoder = coder_stack(DecoderCtor, 6)
num_words = 2
words = torch.randn([num_words, word_width])
qkv_words = qkvs(words, W_Q, W_K, W_V)
encoder = EncoderCtor(num_heads, W_O, word_width)
encoder.eval()
values = encoder(words)
print(values)
print(values.shape)
Refactoring, Stacking Encoders, and Placeholder for Positional Encoding
This step involves a lot of refactoring and cleaning up. Specifically, reordering and cleaning up parameters happens here. Default parameters are added as well. This is also the first time we touch the function to stack six Encoders. Our original code is pretty much useless at this point; thus we simply build a Sequential container of Encoder layers. We obviously verify that it outputs a \(2 \times 512\) vector.
There is still one part of the Encoder we haven’t fleshed out fully: the positional encoding. For the moment, we add a placeholder function positionally_encoded() which we will implement fully going forward.
import torch
import torch.nn as nn
import numpy as np
import math
softmax = torch.nn.Softmax(dim=1)
class DefaultParameters:
DEFAULT_NUM_HEADS = 8
DEFAULT_WORD_WIDTH = 512
DEFAULT_PROJECTION_WIDTH = 64
DEFAULT_SCALE_FACTOR = 100
DEFAULT_FFNN_HIDDEN_LAYER_WIDTH = 2048
NUM_HEADS = 8
WORD_WIDTH = 512
PROJECTION_WIDTH = 64
SCALE_FACTOR = 100
FFNN_HIDDEN_LAYER_WIDTH = 2048
def encoder_stack(num_encoders, w_o):
encoders = np.array(list(map(lambda x: Encoder(w_o,
DefaultParameters.DEFAULT_NUM_HEADS,
DefaultParameters.DEFAULT_WORD_WIDTH), range(num_encoders))))
return nn.Sequential(*encoders)
class SelfAttentionLayer(nn.Module):
def __init__(self, w_q, w_k, w_v):
super(SelfAttentionLayer, self).__init__()
self.w_q = w_q
self.w_k = w_k
self.w_v = w_v
def forward(self, words):
return attention_scores(qkvs(words, self.w_q, self.w_k, self.w_v))
class MultiheadedAttention(nn.Module):
def __init__(self, w_o, num_heads=DefaultParameters.DEFAULT_NUM_HEADS):
super(MultiheadedAttention, self).__init__()
self.w_o = w_o
self.attention_layers = list(map(lambda x: SelfAttentionLayer(W_Q, W_K, W_V), range(num_heads)))
def forward(self, x):
# Concatenating gives [num_words x num_heads * projection_width]
attention_vectors = list(map(lambda attention_layer: attention_layer(x), self.attention_layers))
concatenated_attention_vectors = torch.cat(attention_vectors, dim=1)
scaled_concatenated_attention_vectors = torch.matmul(concatenated_attention_vectors, self.w_o)
return scaled_concatenated_attention_vectors
class Encoder(nn.Module):
def __init__(self, w_o, num_heads=8, word_width=512):
super(Encoder, self).__init__()
self.layer_norm = nn.LayerNorm(word_width)
self.multiheaded_attention_layer = MultiheadedAttention(w_o, num_heads)
self.feedforward_layer = nn.Sequential(
nn.Linear(word_width, DefaultParameters.DEFAULT_FFNN_HIDDEN_LAYER_WIDTH, bias=True),
nn.LeakyReLU(),
nn.Linear(DefaultParameters.DEFAULT_FFNN_HIDDEN_LAYER_WIDTH, word_width, bias=True))
def forward(self, x):
mh_output = self.multiheaded_attention_layer(x)
layer_normed_multihead_output = self.layer_norm(mh_output + x)
ffnn_outputs = torch.stack(
list(map(lambda attention_vector: self.feedforward_layer(attention_vector), layer_normed_multihead_output)))
layer_normed_ffnn_output = self.layer_norm(ffnn_outputs + layer_normed_multihead_output)
return layer_normed_ffnn_output
W_Q = torch.randn([WORD_WIDTH, PROJECTION_WIDTH]) / SCALE_FACTOR
W_K = torch.randn([WORD_WIDTH, PROJECTION_WIDTH]) / SCALE_FACTOR
W_V = torch.randn([WORD_WIDTH, PROJECTION_WIDTH]) / SCALE_FACTOR
W_O = torch.randn([NUM_HEADS * PROJECTION_WIDTH, WORD_WIDTH]) / SCALE_FACTOR
def qkvs(words, w_q, w_k, w_v):
return torch.matmul(words, w_q), torch.matmul(words, w_k), torch.matmul(words, w_v)
def attention_scores(qkvs):
return torch.matmul(softmax(torch.matmul(qkvs[0], torch.transpose(qkvs[1], 0, 1)) / math.sqrt(qkvs[0].shape[1])), qkvs[2])
def positionally_encoded(words):
return words
num_words = 2
words = torch.randn([num_words, WORD_WIDTH])
qkv_words = qkvs(words, W_Q, W_K, W_V)
stack = encoder_stack(6, W_O)
values = stack(positionally_encoded(words))
print(values)
print(values.shape)
# encoder = EncoderCtor(W_O)
# encoder.eval()
# values = encoder(words)
# print(values)
# print(values.shape)
This concludes Part 1 of implementing Transformers using PyTorch. There are a lot of loose ends which we will continue to address in the sequels. The demonstration of the incremental build-up should give you a fair idea of how you can go about implementing models from scratch in PyTorch.
References
tags: Machine Learning - PyTorch - Programming - Deep Learning - Transformers