Total Internal Reflection
Technology and Art
Code
Contact
Plenoxels and Neural Radiance Fields using PyTorch: Part 3
Avishek Sen Gupta on 7 December 2022
This is part of a series of posts breaking down the paper Plenoxels: Radiance Fields without Neural Networks, and providing (hopefully) well-annotated source code to aid in understanding.
The final code has been moved to its own repository at plenoxels-pytorch.
We continue looking at Plenoxels: Radiance Fields without Neural Networks. We start off with understanding Spherical Harmonics, and why we want to use them to capture colour information based on angular direction in 3D space.
Spherical Harmonics
Spherical harmonics essentially define a series (theoretically infinite) of functions defined over a sphere, that is to say, the function values are parameterised by the angles of a spherical coordinate system. It’s essentially like the Fourier Transform, in that the larger the degree of the harmonic, the more accurately a signal on a sphere can be encoded in the series.
\[f(\theta, \phi) = \sum_{l=0}^N \sum_{m=-l}^l C^m_l Y^m_l (\theta, \phi)\]Here, \(N\) is the order, \(C^m_l\) are the coefficients; this results in a linear combination of the basis functions \(Y^m_l\), which represents the target function. How accurately the target is described depends upon how far the series is expanded. The paper expands only to degree 2. This implies that that the number of terms in the above series is \(1+3+5=9\).
The basis functions for degree 2 are listed below:
\[Y^0_0 = \frac{1}{2} \sqrt {\frac{1}{\pi}} \\ Y^{-1}_1 = \frac{1}{2} \sqrt {\frac{3}{\pi}} y \\ Y^0_1 = \frac{1}{2} \sqrt {\frac{3}{\pi}} z \\ Y^1_1 = \frac{1}{2} \sqrt {\frac{3}{\pi}} x \\ Y^{-2}_2 = \frac{1}{2} \sqrt {\frac{15}{\pi}} xy \\ Y^{-1}_2 = \frac{1}{2} \sqrt {\frac{15}{\pi}} yz \\ Y^0_2 = \frac{1}{4} \sqrt {\frac{5}{\pi}} (3z^2 - 1) \\ Y^1_2 = \frac{1}{2} \sqrt {\frac{15}{\pi}} xz \\ Y^2_2 = \frac{1}{4} \sqrt {\frac{15}{\pi}} (x^2 - y^2)\]where \(x\), \(y\), and \(z\) are defined as:
\[x = \text{sin } \theta . \text{cos } \phi \\ y = \text{sin } \theta . \text{sin } \phi \\ z = \text{cos } \theta\]Here is an example of an example 2nd order harmonic with some randomly chosen coefficients. The colours have been modified based on the spherical harmonic value at that specific viewing angle.
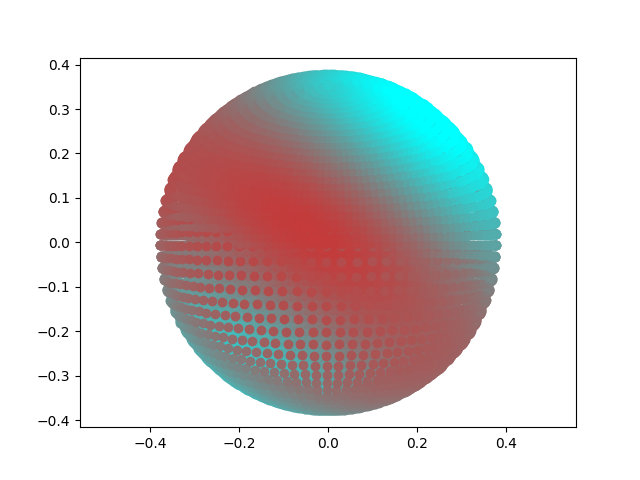
import math
import numpy as np
import torch
import matplotlib.pyplot as plt
class Camera:
def __init__(self, focal_length, center, basis):
camera_center = center.detach().clone()
transposed_basis = torch.transpose(basis, 0, 1)
camera_center[:3] = camera_center[
:3] * -1 # We don't want to multiply the homogenous coordinate component; it needs to remain 1
camera_origin_translation = torch.eye(4, 4)
camera_origin_translation[:, 3] = camera_center
extrinsic_camera_parameters = torch.matmul(torch.inverse(transposed_basis), camera_origin_translation)
intrinsic_camera_parameters = torch.tensor([[focal_length, 0., 0., 0.],
[0., focal_length, 0., 0.],
[0., 0., 1., 0.]])
self.transform = torch.matmul(intrinsic_camera_parameters, extrinsic_camera_parameters)
def to_2D(self, point):
# return torch.transpose(point, 0, 1)
rendered_point = torch.matmul(self.transform, torch.transpose(point, 0, 1))
point_z = rendered_point[2, 0]
return rendered_point / point_z
def camera_basis_from(camera_depth_z_vector):
depth_vector = camera_depth_z_vector[:3] # We just want the inhomogenous parts of the coordinates
# This calculates the projection of the world z-axis onto the surface defined by the camera direction,
# since we want to derive the coordinate system of the camera to be orthogonal without having
# to calculate it manually.
cartesian_z_vector = torch.tensor([0., 0., 1.])
cartesian_z_projection_lambda = torch.dot(depth_vector, cartesian_z_vector) / torch.dot(
depth_vector, depth_vector)
camera_up_vector = cartesian_z_vector - cartesian_z_projection_lambda * depth_vector
# The camera coordinate system now has the direction of camera and the up direction of the camera.
# We need to find the third vector which needs to be orthogonal to both the previous vectors.
# Taking the cross product of these vectors gives us this third component
camera_x_vector = torch.linalg.cross(depth_vector, camera_up_vector)
inhomogeneous_basis = torch.stack([camera_x_vector, camera_up_vector, depth_vector, torch.tensor([0., 0., 0.])])
homogeneous_basis = torch.hstack((inhomogeneous_basis, torch.tensor([[0.], [0.], [0.], [1.]])))
homogeneous_basis[0] = unit_vector(homogeneous_basis[0])
homogeneous_basis[1] = unit_vector(homogeneous_basis[1])
homogeneous_basis[2] = unit_vector(homogeneous_basis[2])
return homogeneous_basis
def basis_from_depth(look_at, camera_center):
depth_vector = torch.sub(look_at, camera_center)
depth_vector[3] = 1.
return camera_basis_from(depth_vector)
def unit_vector(camera_basis_vector):
return camera_basis_vector / math.sqrt(
pow(camera_basis_vector[0], 2) +
pow(camera_basis_vector[1], 2) +
pow(camera_basis_vector[2], 2))
def plot(style="bo"):
return lambda p: plt.plot(p[0][0], p[1][0], style)
def line(marker="o"):
return lambda p1, p2: plt.plot([p1[0][0], p2[0][0]], [p1[1][0], p2[1][0]], marker="o")
look_at = torch.tensor([0., 0., 0., 1])
camera_center = torch.tensor([10., -10., 0., 1.])
focal_length = 1
camera_basis = basis_from_depth(look_at, camera_center)
camera = Camera(focal_length, camera_center, camera_basis)
Y_0_0 = 0.5 * math.sqrt(1. / math.pi)
Y_m1_1 = lambda theta, phi: 0.5 * math.sqrt(3. / math.pi) * math.sin(theta) * math.sin(phi)
Y_0_1 = lambda theta, phi: 0.5 * math.sqrt(3. / math.pi) * math.cos(theta)
Y_1_1 = lambda theta, phi: 0.5 * math.sqrt(3. / math.pi) * math.sin(theta) * math.cos(phi)
Y_m2_2 = lambda theta, phi: 0.5 * math.sqrt(15. / math.pi) * math.sin(theta) * math.cos(phi) * math.sin(
theta) * math.sin(phi)
Y_m1_2 = lambda theta, phi: 0.5 * math.sqrt(15. / math.pi) * math.sin(theta) * math.sin(phi) * math.cos(theta)
Y_0_2 = lambda theta, phi: 0.25 * math.sqrt(5. / math.pi) * (3 * math.cos(theta) * math.cos(theta) - 1)
Y_1_2 = lambda theta, phi: 0.5 * math.sqrt(15. / math.pi) * math.sin(theta) * math.cos(phi) * math.cos(theta)
Y_2_2 = lambda theta, phi: 0.25 * math.sqrt(15. / math.pi) * (
pow(math.sin(theta) * math.cos(phi), 2) - pow(math.sin(theta) * math.sin(phi), 2))
def harmonic(C_0_0, C_m1_1, C_0_1, C_1_1, C_m2_2, C_m1_2, C_0_2, C_1_2, C_2_2):
return lambda theta, phi: C_0_0 * Y_0_0 + C_m1_1 * Y_m1_1(theta, phi) + C_0_1 * Y_0_1(theta, phi) + C_1_1 * Y_1_1(
theta, phi) + C_m2_2 * Y_m2_2(theta, phi) + C_m1_2 * Y_m1_2(theta, phi) + C_0_2 * Y_0_2(theta,
phi) + C_1_2 * Y_1_2(
theta, phi) + C_2_2 * Y_2_2(theta, phi)
test_harmonic = harmonic(1, 2, 3, 4, 5, 6, 7, 8, 1)
radius = 5.
plt.figure()
plt.axis("equal")
i = math.pi / 2
j = math.pi / 2
x = radius * math.sin(i) * math.cos(j)
y = radius * math.sin(i) * math.sin(j)
z = radius * math.cos(i)
print(torch.tensor([[x,y,z,1.]]))
for theta in np.linspace(0, 2. * math.pi, 100):
for phi in np.linspace(0, 2. * math.pi, 100):
value = test_harmonic(theta, phi) / 20. + 0.5
if value > 1.0:
value = 1.
x = radius * math.sin(theta) * math.cos(phi)
y = radius * math.sin(theta) * math.sin(phi)
z = radius * math.cos(theta)
d = camera.to_2D(torch.tensor([[x,y,z,1.]]))
plt.plot(d[0][0], d[1][0], marker="o", color=(1 - value, value, value))
plt.show()
Incorporating Spherical Harmonics
Let’s incorporate spherical harmonics into our rendering model. We have reached the point where each voxel in the world needs to be represented by a full-blown tensor of opacity and three set of 9 harmonic coefficients, hence 28 numbers.
Also, we are no longer calculating a single density; we are calculating the intensity for each colour channel. It is the same calculation, however the colour will now be calculated using the spherical harmonic functions.
import math
import numpy as np
import torch
import matplotlib.pyplot as plt
import functools
class Camera:
def __init__(self, focal_length, center, basis):
self.basis = basis
camera_center = center.detach().clone()
transposed_basis = torch.transpose(basis, 0, 1)
camera_center[:3] = camera_center[
:3] * -1 # We don't want to multiply the homogenous coordinate component; it needs to remain 1
camera_origin_translation = torch.eye(4, 4)
camera_origin_translation[:, 3] = camera_center
extrinsic_camera_parameters = torch.matmul(torch.inverse(transposed_basis), camera_origin_translation)
intrinsic_camera_parameters = torch.tensor([[focal_length, 0., 0., 0.],
[0., focal_length, 0., 0.],
[0., 0., 1., 0.]])
self.transform = torch.matmul(intrinsic_camera_parameters, extrinsic_camera_parameters)
def to_2D(self, point):
rendered_point = torch.matmul(self.transform, torch.transpose(point, 0, 1))
point_z = rendered_point[2, 0]
return rendered_point / point_z
def viewing_angle(self):
camera_basis_z = self.basis[2][:3]
camera_basis_theta = math.atan(camera_basis_z[1] / camera_basis_z[2])
camera_basis_phi = math.atan(camera_basis_z[2] / camera_basis_z.norm())
return torch.tensor([camera_basis_theta, camera_basis_phi])
def camera_basis_from(camera_depth_z_vector):
depth_vector = camera_depth_z_vector[:3] # We just want the inhomogenous parts of the coordinates
# This calculates the projection of the world z-axis onto the surface defined by the camera direction,
# since we want to derive the coordinate system of the camera to be orthogonal without having
# to calculate it manually.
cartesian_z_vector = torch.tensor([0., 0., 1.])
cartesian_z_projection_lambda = torch.dot(depth_vector, cartesian_z_vector) / torch.dot(
depth_vector, depth_vector)
camera_up_vector = cartesian_z_vector - cartesian_z_projection_lambda * depth_vector
# The camera coordinate system now has the direction of camera and the up direction of the camera.
# We need to find the third vector which needs to be orthogonal to both the previous vectors.
# Taking the cross product of these vectors gives us this third component
camera_x_vector = torch.linalg.cross(depth_vector, camera_up_vector)
inhomogeneous_basis = torch.stack([camera_x_vector, camera_up_vector, depth_vector, torch.tensor([0., 0., 0.])])
homogeneous_basis = torch.hstack((inhomogeneous_basis, torch.tensor([[0.], [0.], [0.], [1.]])))
homogeneous_basis[0] = unit_vector(homogeneous_basis[0])
homogeneous_basis[1] = unit_vector(homogeneous_basis[1])
homogeneous_basis[2] = unit_vector(homogeneous_basis[2])
return homogeneous_basis
def basis_from_depth(look_at, camera_center):
depth_vector = torch.sub(look_at, camera_center)
depth_vector[3] = 1.
return camera_basis_from(depth_vector)
def unit_vector(camera_basis_vector):
return camera_basis_vector / math.sqrt(
pow(camera_basis_vector[0], 2) +
pow(camera_basis_vector[1], 2) +
pow(camera_basis_vector[2], 2))
def plot(style="bo"):
return lambda p: plt.plot(p[0][0], p[1][0], style)
def line(marker="o"):
return lambda p1, p2: plt.plot([p1[0][0], p2[0][0]], [p1[1][0], p2[1][0]], marker="o")
HALF_SQRT_3_BY_PI = 0.5 * math.sqrt(3. / math.pi)
HALF_SQRT_15_BY_PI = 0.5 * math.sqrt(15. / math.pi)
QUARTER_SQRT_15_BY_PI = 0.25 * math.sqrt(15. / math.pi)
QUARTER_SQRT_5_BY_PI = 0.25 * math.sqrt(5. / math.pi)
Y_0_0 = 0.5 * math.sqrt(1. / math.pi)
Y_m1_1 = lambda theta, phi: HALF_SQRT_3_BY_PI * math.sin(theta) * math.sin(phi)
Y_0_1 = lambda theta, phi: HALF_SQRT_3_BY_PI * math.cos(theta)
Y_1_1 = lambda theta, phi: HALF_SQRT_3_BY_PI * math.sin(theta) * math.cos(phi)
Y_m2_2 = lambda theta, phi: HALF_SQRT_15_BY_PI * math.sin(theta) * math.cos(phi) * math.sin(
theta) * math.sin(phi)
Y_m1_2 = lambda theta, phi: HALF_SQRT_15_BY_PI * math.sin(theta) * math.sin(phi) * math.cos(theta)
Y_0_2 = lambda theta, phi: QUARTER_SQRT_5_BY_PI * (3 * math.cos(theta) * math.cos(theta) - 1)
Y_1_2 = lambda theta, phi: HALF_SQRT_15_BY_PI * math.sin(theta) * math.cos(phi) * math.cos(theta)
Y_2_2 = lambda theta, phi: QUARTER_SQRT_15_BY_PI * (
pow(math.sin(theta) * math.cos(phi), 2) - pow(math.sin(theta) * math.sin(phi), 2))
def harmonic(C_0_0, C_m1_1, C_0_1, C_1_1, C_m2_2, C_m1_2, C_0_2, C_1_2, C_2_2):
return lambda theta, phi: C_0_0 * Y_0_0 + C_m1_1 * Y_m1_1(theta, phi) + C_0_1 * Y_0_1(theta, phi) + C_1_1 * Y_1_1(
theta, phi) + C_m2_2 * Y_m2_2(theta, phi) + C_m1_2 * Y_m1_2(theta, phi) + C_0_2 * Y_0_2(theta,
phi) + C_1_2 * Y_1_2(
theta, phi) + C_2_2 * Y_2_2(theta, phi)
def rgb_harmonics(rgb_harmonic_coefficients):
red_harmonic = harmonic(*rgb_harmonic_coefficients[:9])
green_harmonic = harmonic(*rgb_harmonic_coefficients[9:18])
blue_harmonic = harmonic(*rgb_harmonic_coefficients[18:])
return (red_harmonic, green_harmonic, blue_harmonic)
class VoxelGrid:
VOXEL_DIMENSION = 28
def __init__(self, x, y, z):
self.grid_x = x
self.grid_y = y
self.grid_z = z
self.default_voxel = torch.rand([VoxelGrid.VOXEL_DIMENSION])
self.empty_voxel = torch.zeros([VoxelGrid.VOXEL_DIMENSION])
self.default_voxel[0] = 0.005
self.voxel_grid = torch.zeros([self.grid_x, self.grid_y, self.grid_z, VoxelGrid.VOXEL_DIMENSION])
def random_voxel(self):
voxel = torch.rand([VoxelGrid.VOXEL_DIMENSION])
voxel[0] = 0.01
return voxel
def at(self, x, y, z):
if self.is_outside(x, y, z):
return self.empty_voxel
else:
return self.voxel_grid[int(x), int(y), int(z)]
def is_inside(self, x, y, z):
if (0 <= x < self.grid_x and
0 <= y < self.grid_y and
0 <= z < self.grid_z):
return True
def is_outside(self, x, y, z):
return not self.is_inside(x, y, z)
def channel_opacity(self, position_distance_density_color_tensors, viewing_angle):
position_distance_density_color_vectors = position_distance_density_color_tensors.numpy()
number_of_samples = len(position_distance_density_color_vectors)
transmittances = list(map(lambda i: functools.reduce(
lambda acc, j: acc + math.exp(
- position_distance_density_color_vectors[j, 4] * position_distance_density_color_vectors[j, 3]),
range(0, i), 0.), range(1, number_of_samples + 1)))
color_densities = torch.zeros([3])
for index, transmittance in enumerate(transmittances):
if (position_distance_density_color_vectors[index, 4] == 0.):
continue
# density += (transmittance - transmittances[index + 1]) * position_distance_density_color_vectors[index, 5]
red_harmonic, green_harmonic, blue_harmonic = rgb_harmonics(
position_distance_density_color_tensors[index, 5:])
r = red_harmonic(viewing_angle[0], viewing_angle[1])
g = green_harmonic(viewing_angle[0], viewing_angle[1])
b = blue_harmonic(viewing_angle[0], viewing_angle[1])
base_transmittance = transmittance * (1. - math.exp(
- position_distance_density_color_vectors[index, 4] * position_distance_density_color_vectors[
index, 3]))
# if (base_transmittance > 1. or base_transmittance < 0.):
# raise Exception(f"Transmittance was {base_transmittance}")
# if (r > 1. or r < 0. or g > 1. or g < 0. or b > 1. or b < 0.):
# raise Exception(f"Harmonic values were ({r}, {g}, {b})")
color_densities += torch.tensor([base_transmittance * r, base_transmittance * g, base_transmittance * b])
return color_densities
def build_solid_cube(self):
for i in range(13, self.grid_x - 13):
for j in range(13, self.grid_y - 13):
for k in range(13, self.grid_z - 13):
self.voxel_grid[i, j, k] = self.default_voxel
def build_random_hollow_cube(self):
self.build_hollow_cube(self.random_voxel)
def build_monochrome_hollow_cube(self):
self.build_hollow_cube(lambda: self.random_voxel)
def build_hollow_cube(self, make_voxel):
self.build_random_hollow_cube2(make_voxel, torch.tensor([10, 10, 10, 20, 20, 20]))
def build_random_hollow_cube2(self, make_voxel, cube_spec):
x, y, z, dx, dy, dz = cube_spec
voxel_1, voxel_2, voxel_3, voxel_4, voxel_5, voxel_6 = make_voxel(), make_voxel(), make_voxel(), make_voxel(), make_voxel(), make_voxel()
for i in range(x, x + dx + 1):
for j in range(y, y + dy + 1):
self.voxel_grid[i, j, z] = voxel_1
for i in range(x, x + dx + 1):
for j in range(y, y + dy + 1):
self.voxel_grid[i, j, z + dz] = voxel_2
for i in range(y, y + dy + 1):
for j in range(z, z + dz + 1):
self.voxel_grid[x, i, j] = voxel_3
for i in range(y, y + dy + 1):
for j in range(z, z + dz + 1):
self.voxel_grid[x + dx, i, j] = voxel_4
for i in range(z, z + dz + 1):
for j in range(x, x + dx + 1):
self.voxel_grid[j, y, i] = voxel_5
for i in range(z, z + dz + 1):
for j in range(x, x + dx + 1):
self.voxel_grid[j, y + dy, i] = voxel_6
def density(self, ray_samples_with_distances, viewing_angle):
collected_voxels = []
for ray_sample in ray_samples_with_distances:
x = ray_sample[0]
y = ray_sample[1]
z = ray_sample[2]
x_0, x_1 = int(x), int(x) + 1
y_0, y_1 = int(y), int(y) + 1
z_0, z_1 = int(z), int(z) + 1
x_d = (x - x_0) / (x_1 - x_0)
y_d = (y - y_0) / (y_1 - y_0)
z_d = (z - z_0) / (z_1 - z_0)
c_000 = self.at(x_0, y_0, z_0)
c_001 = self.at(x_0, y_0, z_1)
c_010 = self.at(x_0, y_1, z_0)
c_011 = self.at(x_0, y_1, z_1)
c_100 = self.at(x_1, y_0, z_0)
c_101 = self.at(x_1, y_0, z_1)
c_110 = self.at(x_1, y_1, z_0)
c_111 = self.at(x_1, y_1, z_1)
c_00 = c_000 * (1 - x_d) + c_100 * x_d
c_01 = c_001 * (1 - x_d) + c_101 * x_d
c_10 = c_010 * (1 - x_d) + c_110 * x_d
c_11 = c_011 * (1 - x_d) + c_111 * x_d
c_0 = c_00 * (1 - y_d) + c_10 * y_d
c_1 = c_01 * (1 - y_d) + c_11 * y_d
c = c_0 * (1 - z_d) + c_1 * z_d
collected_voxels.append(c)
return self.channel_opacity(torch.cat([ray_samples_with_distances, torch.stack(collected_voxels)], 1),
viewing_angle)
class Renderer:
def __init__(self, camera, view_spec, ray_spec):
self.camera = camera
self.ray_length = ray_spec[0]
self.num_ray_samples = ray_spec[1]
self.x_1, self.x_2 = view_spec[0], view_spec[1]
self.y_1, self.y_2 = view_spec[2], view_spec[3]
self.num_view_samples = view_spec[4]
def render(self, plt):
camera_basis_x = camera.basis[0][:3]
camera_basis_y = camera.basis[1][:3]
viewing_angle = camera.viewing_angle()
camera_center_inhomogenous = camera_center[:3]
fig2 = plt.figure()
for i in np.linspace(self.x_1, self.x_2, self.num_view_samples):
for j in np.linspace(self.y_1, self.y_2, self.num_view_samples):
ray_screen_intersection = camera_basis_x * i + camera_basis_y * j
unit_ray = unit_vector(ray_screen_intersection - camera_center_inhomogenous)
ray_samples = []
# To remove artifacts, set ray step samples to be higher, like 200
for k in np.linspace(0, self.ray_length, self.num_view_samples):
ray_endpoint = camera_center_inhomogenous + unit_ray * k
ray_x, ray_y, ray_z = ray_endpoint
if (world.is_outside(ray_x, ray_y, ray_z)):
continue
# We are in the box
ray_samples.append([ray_x, ray_y, ray_z])
unique_ray_samples = torch.unique(torch.tensor(ray_samples), dim=0)
if (len(unique_ray_samples) <= 1):
continue
t1 = unique_ray_samples[:-1]
t2 = unique_ray_samples[1:]
consecutive_sample_distances = (t1 - t2).pow(2).sum(1).sqrt()
# Make 1D tensor into 2D tensor
ray_samples_with_distances = torch.cat([t1, torch.reshape(consecutive_sample_distances, (-1, 1))], 1)
color_densities = world.density(ray_samples_with_distances, viewing_angle)
print(color_densities)
plt.plot(i, j, marker="o", color=(1. - torch.clamp(color_densities, min=0, max=1).numpy()))
plt.show()
print("Done!!")
GRID_X = 40
GRID_Y = 40
GRID_Z = 40
world = VoxelGrid(GRID_X, GRID_Y, GRID_Z)
# world.build_solid_cube()
# world.build_random_hollow_cube()
world.build_random_hollow_cube2(world.random_voxel, torch.tensor([10, 10, 10, 20, 20, 20]))
world.build_random_hollow_cube2(world.random_voxel, torch.tensor([15, 15, 15, 10, 10, 10]))
camera_look_at = torch.tensor([0., 0., 0., 1])
# camera_center = torch.tensor([-60., 5., 15., 1.])
# camera_center = torch.tensor([-10., -10., 15., 1.])
camera_center = torch.tensor([-20., -10., 40., 1.])
# camera_center = torch.tensor([-20., -20., 40., 1.])
focal_length = 1.
camera_basis = basis_from_depth(camera_look_at, camera_center)
camera = Camera(focal_length, camera_center, camera_basis)
plt.rcParams['axes.facecolor'] = 'black'
plt.axis("equal")
fig1 = plt.figure()
for i in range(0, world.grid_x):
for j in range(0, world.grid_y):
for k in range(0, world.grid_z):
voxel = world.at(i, j, k)
if (voxel[0] == 0.):
continue
d = camera.to_2D(torch.tensor([[i, j, k, 1.]]))
plt.plot(d[0][0], d[1][0], marker="o")
plt.show()
r = Renderer(camera, torch.tensor([-35, 30, -15, 60, 100]), torch.tensor([100, 100]))
r.render(plt)
We also take this opportunity to do some obvious optimisations, like precomputing the spherical harmonic constants.
Example Renders using Spherical Harmonics
Just to recap how our volume renderer has progressed, here is an evolution sequence.
Non-rendered voxel grid
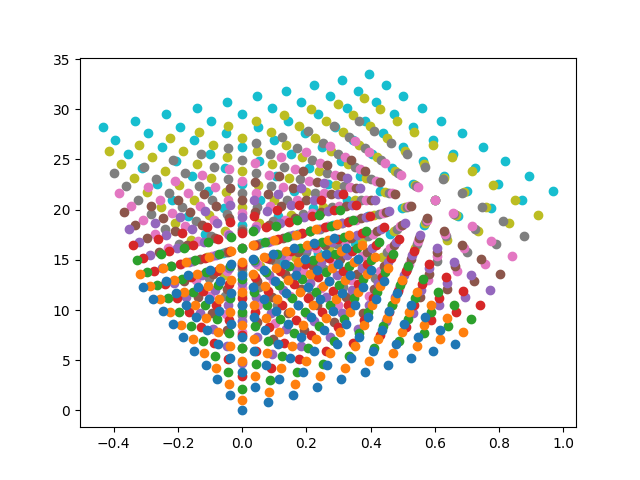Simple density-based voxel rendering
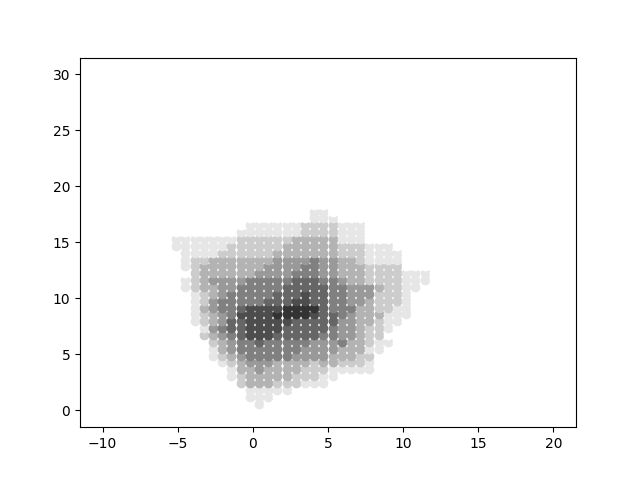Volumentric rendering without Linear Interpolation
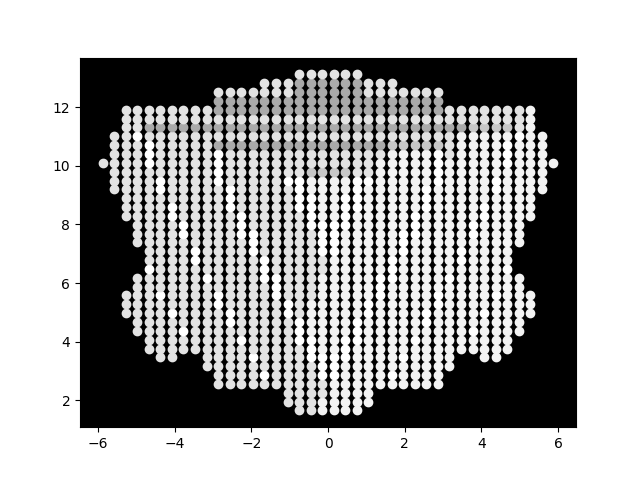Volumentric rendering with Linear Interpolation
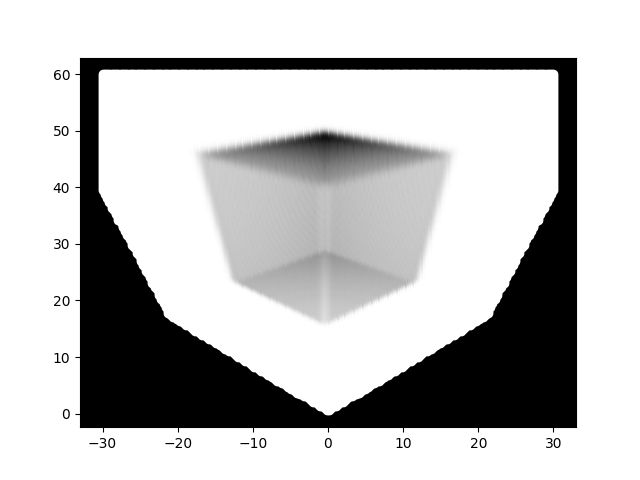Volumentric rendering with Linear Interpolation and Spherical Harmonics
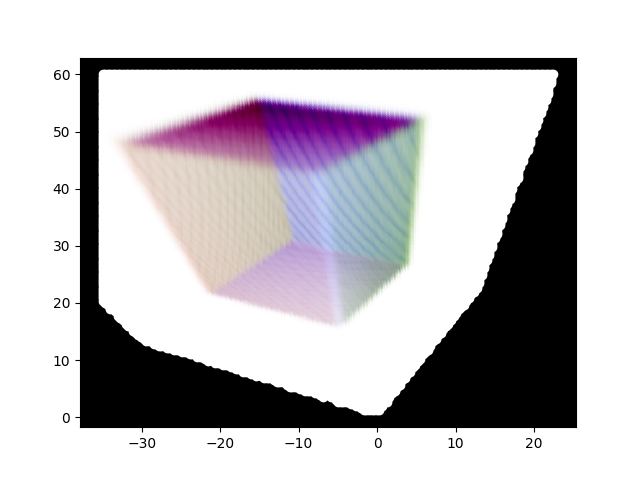
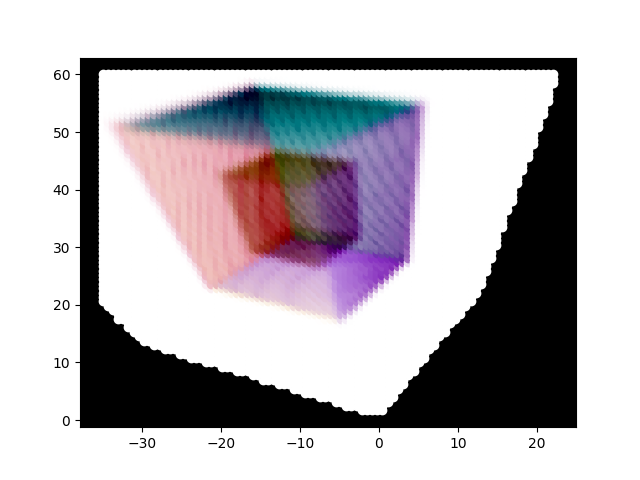
Our volumetric renderer is mostly ready; there might be some smaller changes that we will keep doing. However, the sequels will start looking at the actual reason we are looking at this paper, namely, the optimisation of the spherical harmonics to capture the voxel geometry of the scene. This will require us to first calculate loss, and that is where we will start next time.
References
tags: Machine Learning - PyTorch - Programming - Neural Radiance Fields - Machine Vision